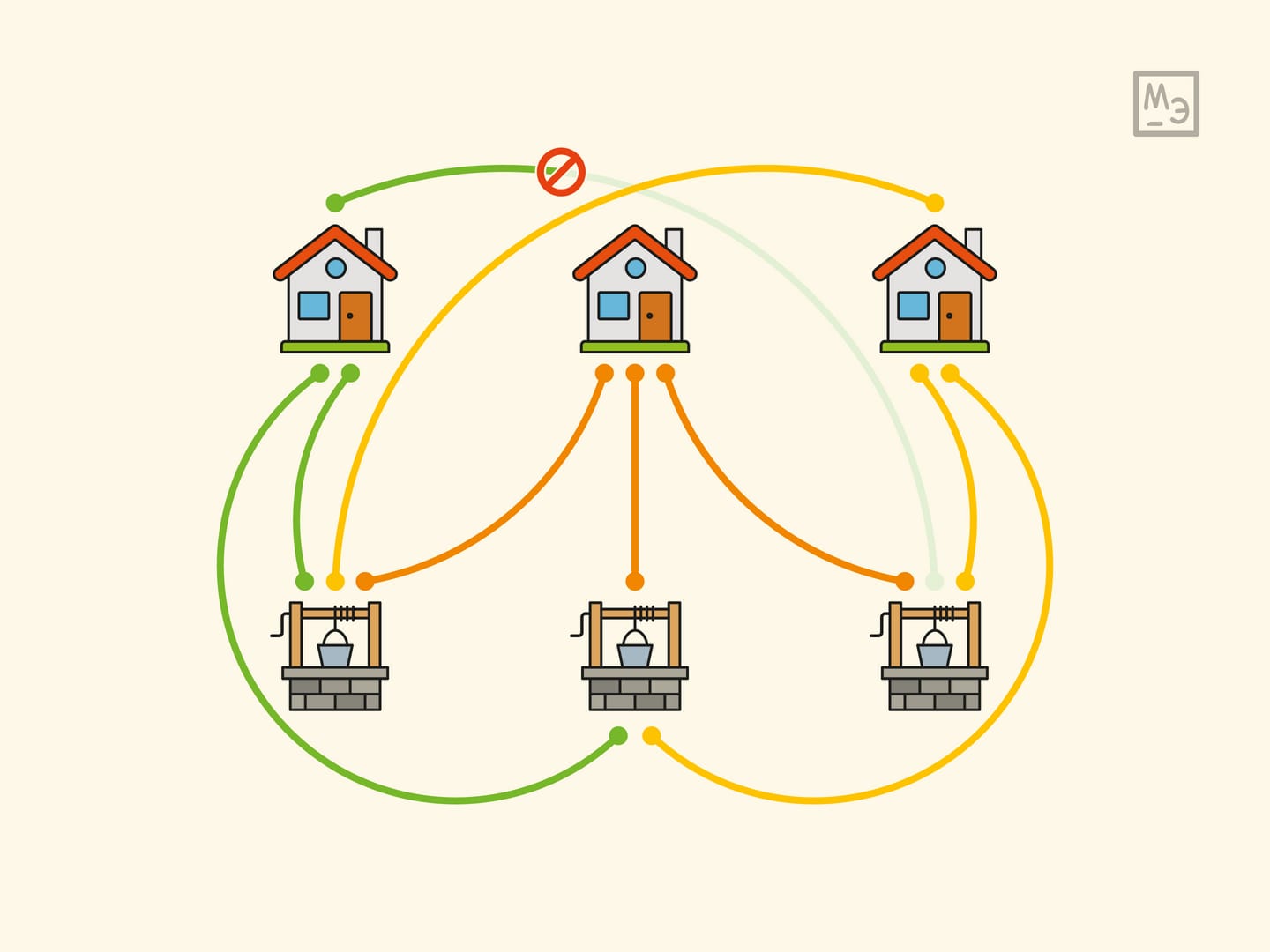
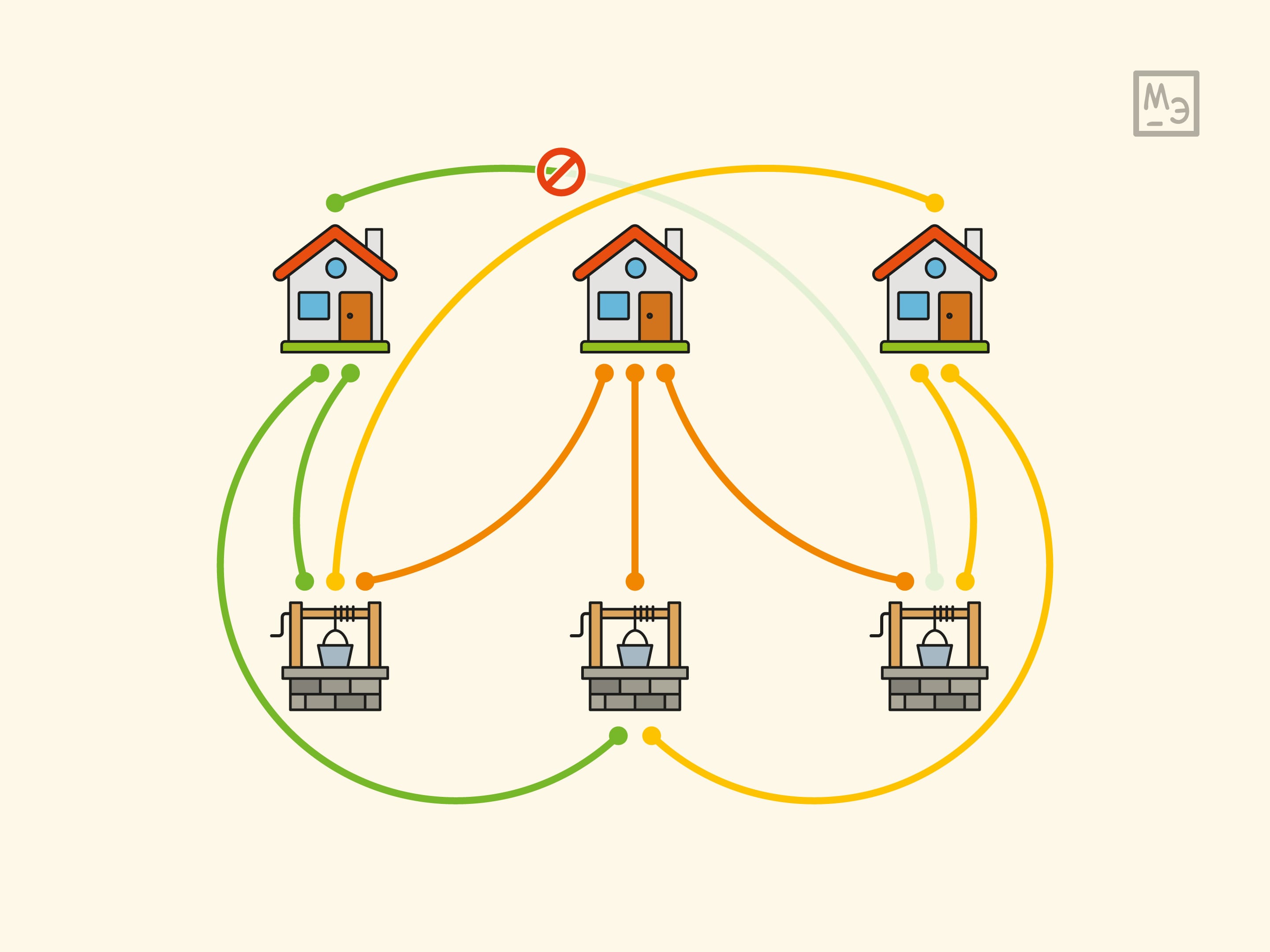
На поверхности кружки с ручкой нарисовано три домика и три колодца. Попробуйте маркером провести дорожки от каждого домика к каждому колодцу так, чтобы дорожки не пересекались.
Естественно желание начать рисовать не на кружке, а на листочке бумаги. И если порисовать разные картинки на листочке, то через некоторое время не остаётся сомнений в том, что граф $K_{3,3}$ ($3$ домика и $3$ колодца, каждый домик соединён дорожкой с каждым колодцем; полный двудольный граф) «не планарен», т. е. не может быть нарисован на плоскости без пересечения рёбер.
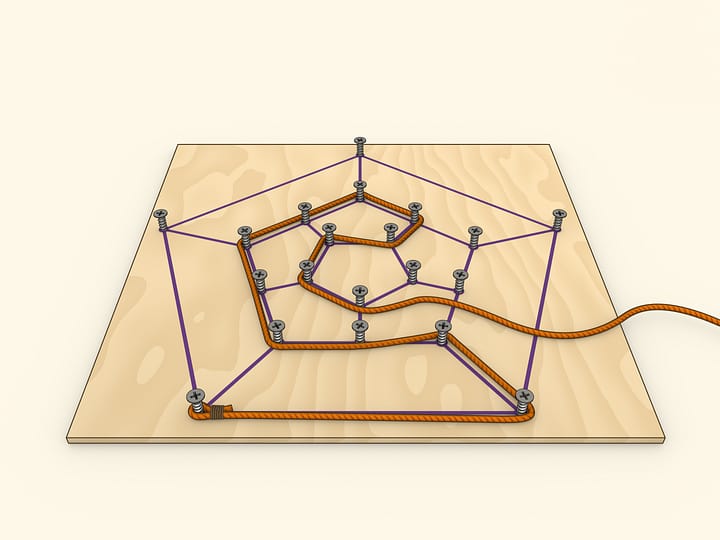
Порисовав, можно убедиться, что невозможно отметить на плоскости $5$ точек и соединить каждую с каждой непересекающимися путями: граф $K_5$ — полный граф на $5$ вершинах — также не является планарным.
Ясно, что раз непланарен граф $K_5$, то непланарен и любой содержащий его граф: например, полный граф на $N$ вершинах при $N > 5$. То же можно сказать про граф, содержащий $K_{3,3}$. Замечательно, что по сути это единственные препятствия к планарности! Это утверждает теорема Куратовского $(1930)$: граф является планарным тогда и только тогда, когда он не содержит подграфа, получающегося из $K_5$ или $K_{3,3}$ подразбиением рёбер.
Провести последнюю дорожку на листочке можно, если нарисовать один мостик, по которому одна дорога проходит над другой. Но это уже будет не решением задачи на плоскости, а решением задачи на кружке. В качестве мостика можно воспользоваться ручкой!
С топологической точки зрения поверхность кружки является тором (поверхностью бублика). В тор можно, как говорят, «вложить» граф $K_{3,3}$, можно в него вложить и граф $K_5$. И даже граф $K_7$ может быть нарисован на торе — это по сути представлено в фильме Раскраски и многогранники. Переход от раскрасок к графам такой: внутри «страны» каждого из $7$ цветов ставится по вершине, а рёбра проводятся через участки общей границы.
Конечно, и на торе можно нарисовать совсем не любой граф (проще всего это понять при помощи версии формулы Эйлера для тора). Из теоремы Робертсона—Сеймура следует, что существует описание графов, вложимых в какую-то конкретную поверхность, в духе теоремы Куратовского — предъявлением графов, которые нельзя нарисовать на ней. Но даже для тора минимальный список препятствий состоит уже не из двух графов, а более чем из $10\,000$ (и не все они ещё найдены). А вот сделать математический сувенир, нарисовав или распечатав на кружке три домика и три колодца, можно уже сейчас.
Другие модели раздела «Комбинаторика, вероятность, случайность»
