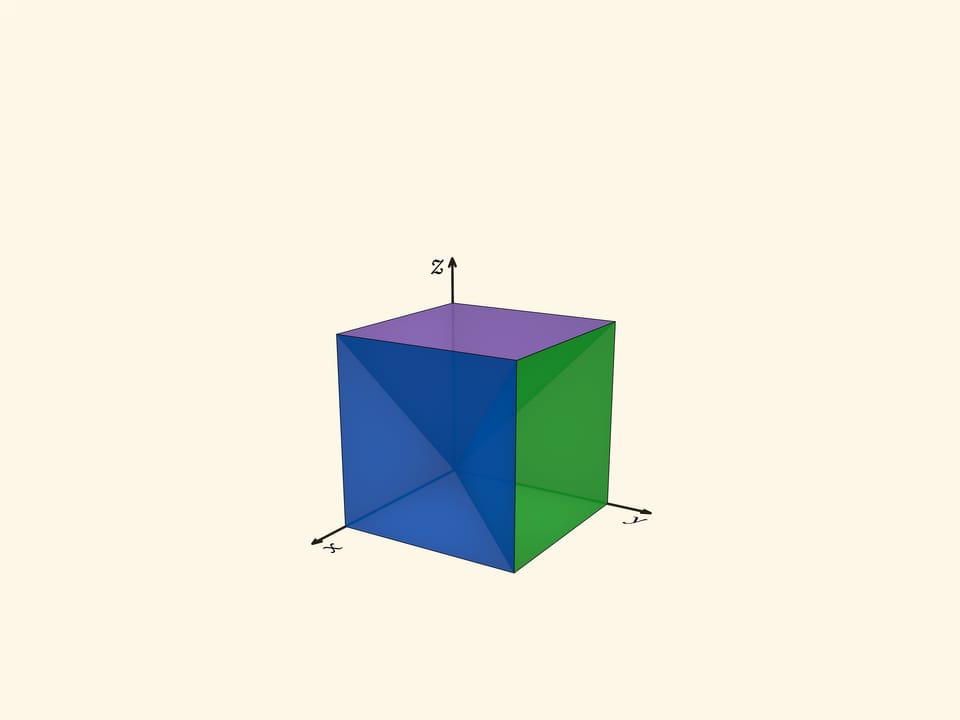
Можно ли куб разрезать на три равные пирамиды? Можно, но сходу — неочевидно как. А вот модель из трёх одинаковых пирамид, из которых составляется куб, хоть и простая, но полезная. В частности, иллюстрирует тот факт, что объём пирамиды равен трети объёма призмы.
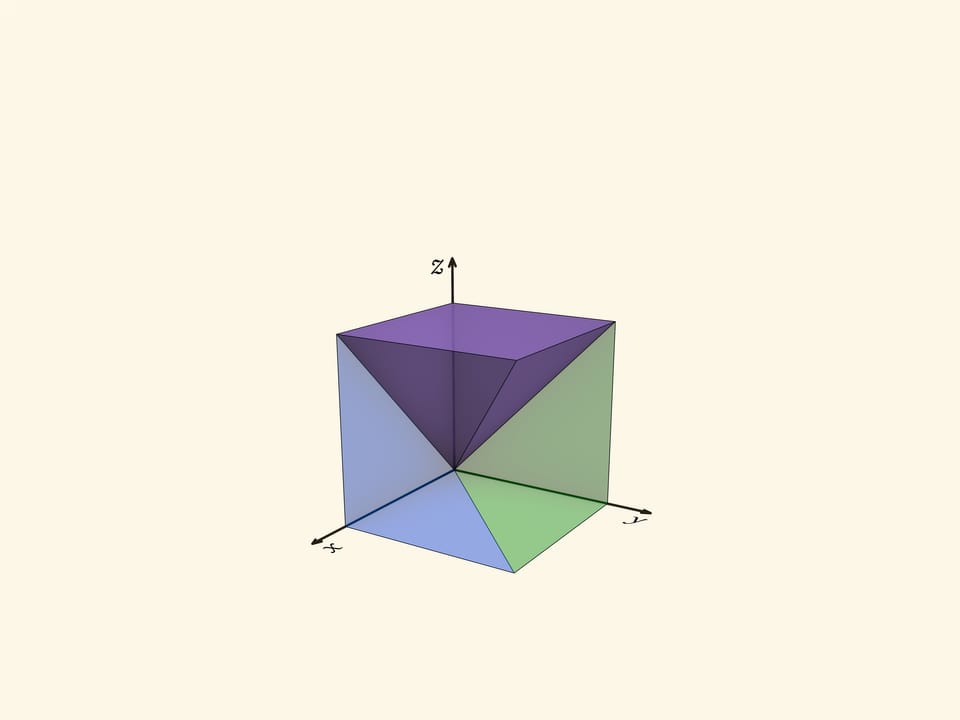
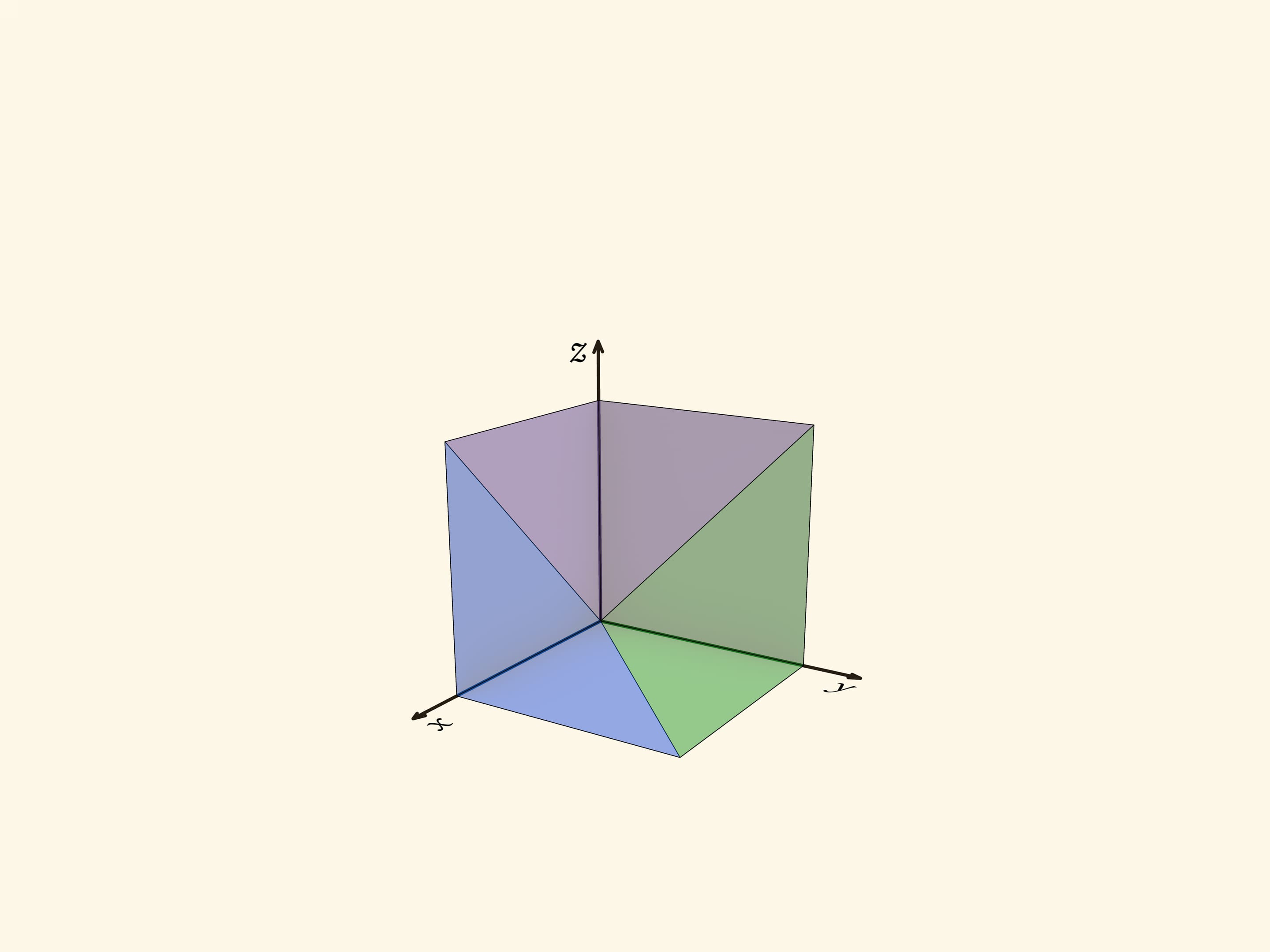
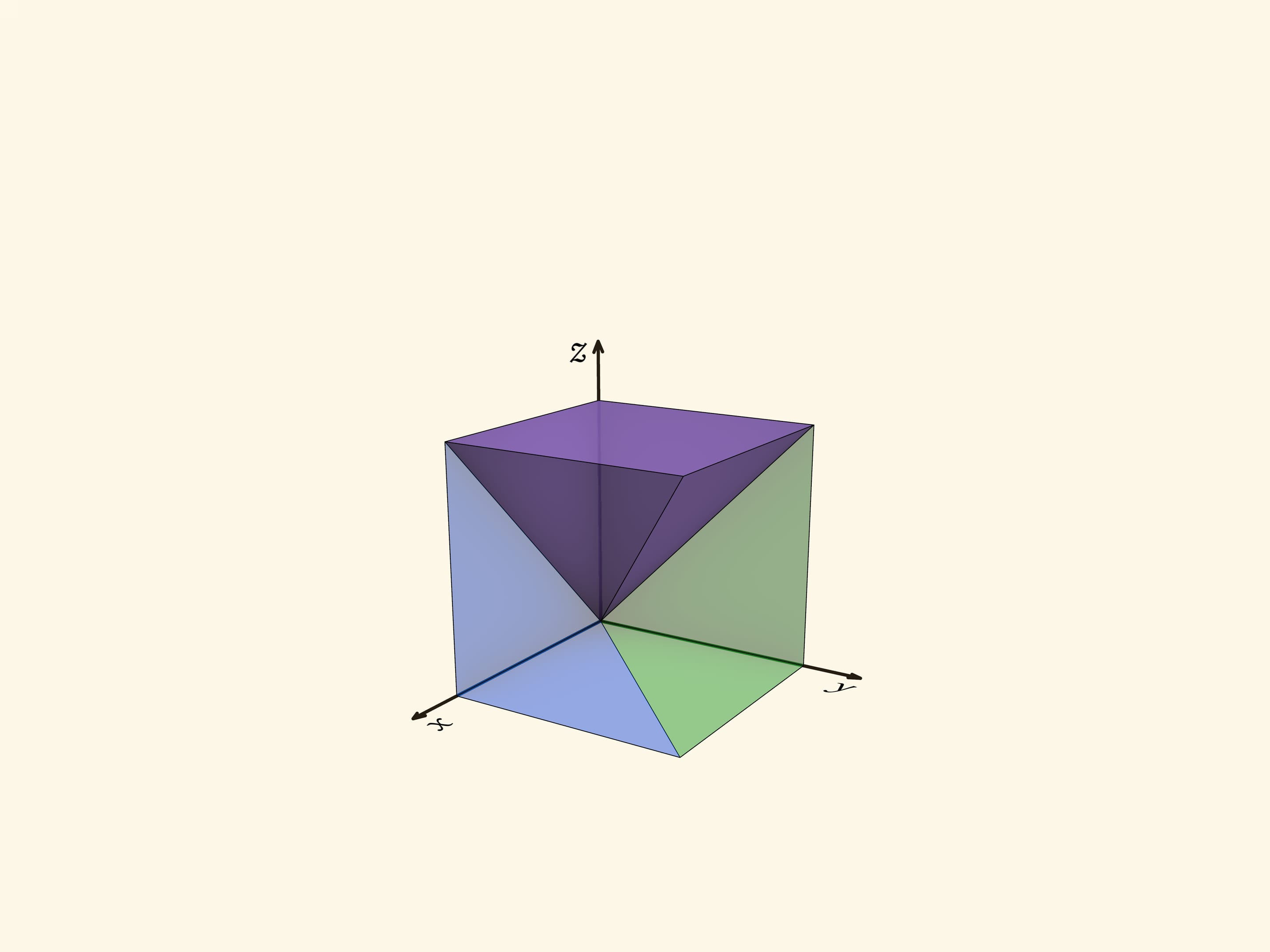
Куб делится на три одинаковые пирамиды с общей вершиной: основания пирамид — три грани куба, не содержащие эту вершину; рёбра — отрезки, проведённые из общей вершины в вершины граней. Пирамиды получаются четырёхугольные, у каждой есть ребро, перпендикулярное основанию. Диагональ куба — общее ребро всех трёх пирамид.
На это разбиение можно смотреть и с алгебраической точки зрения.
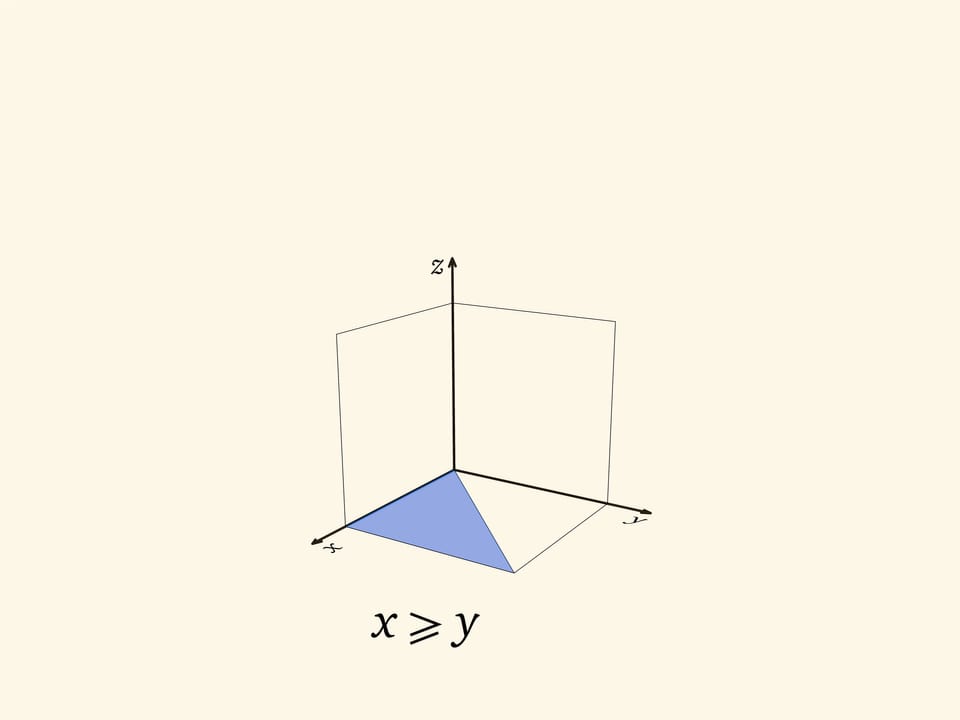
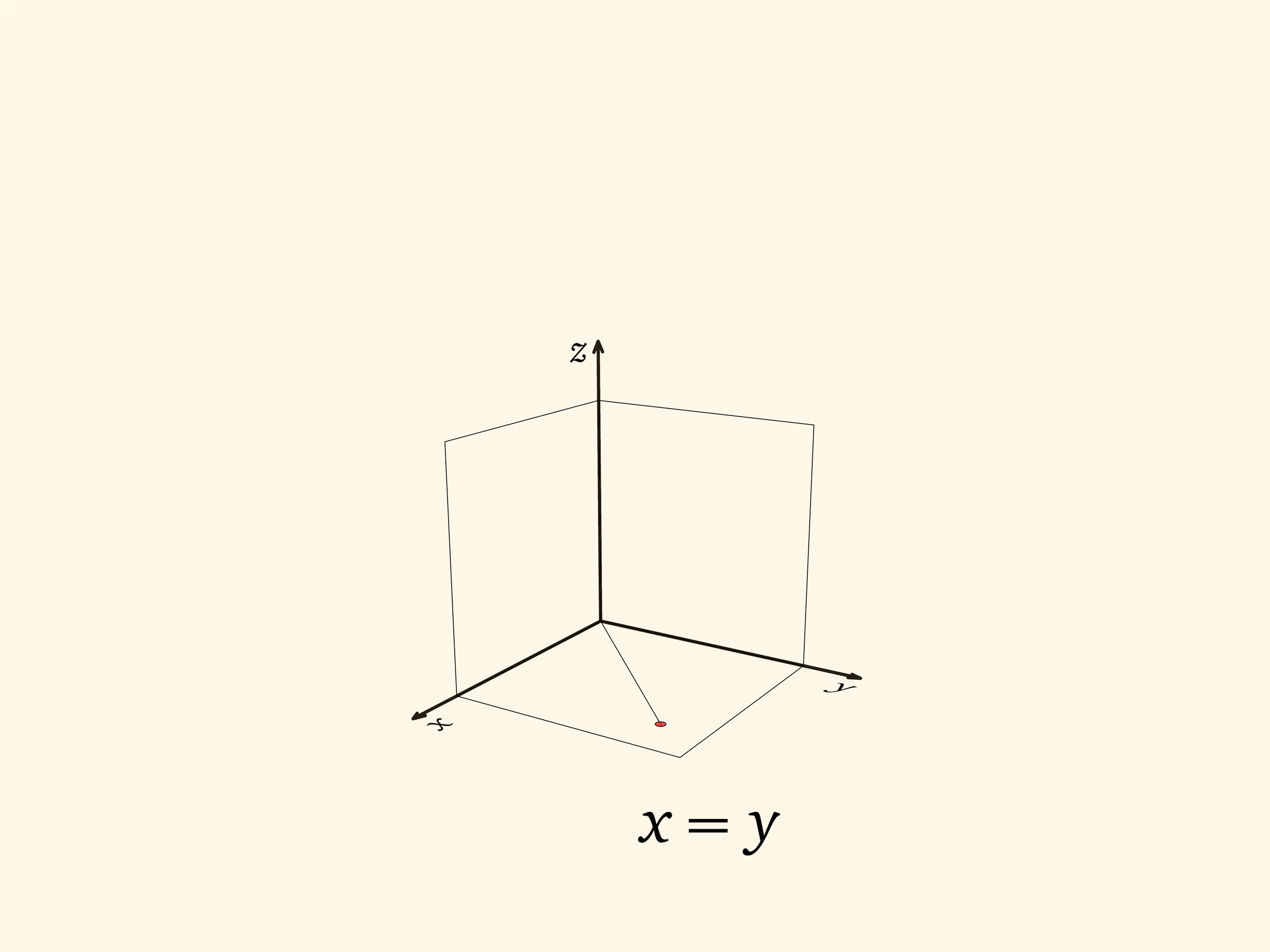
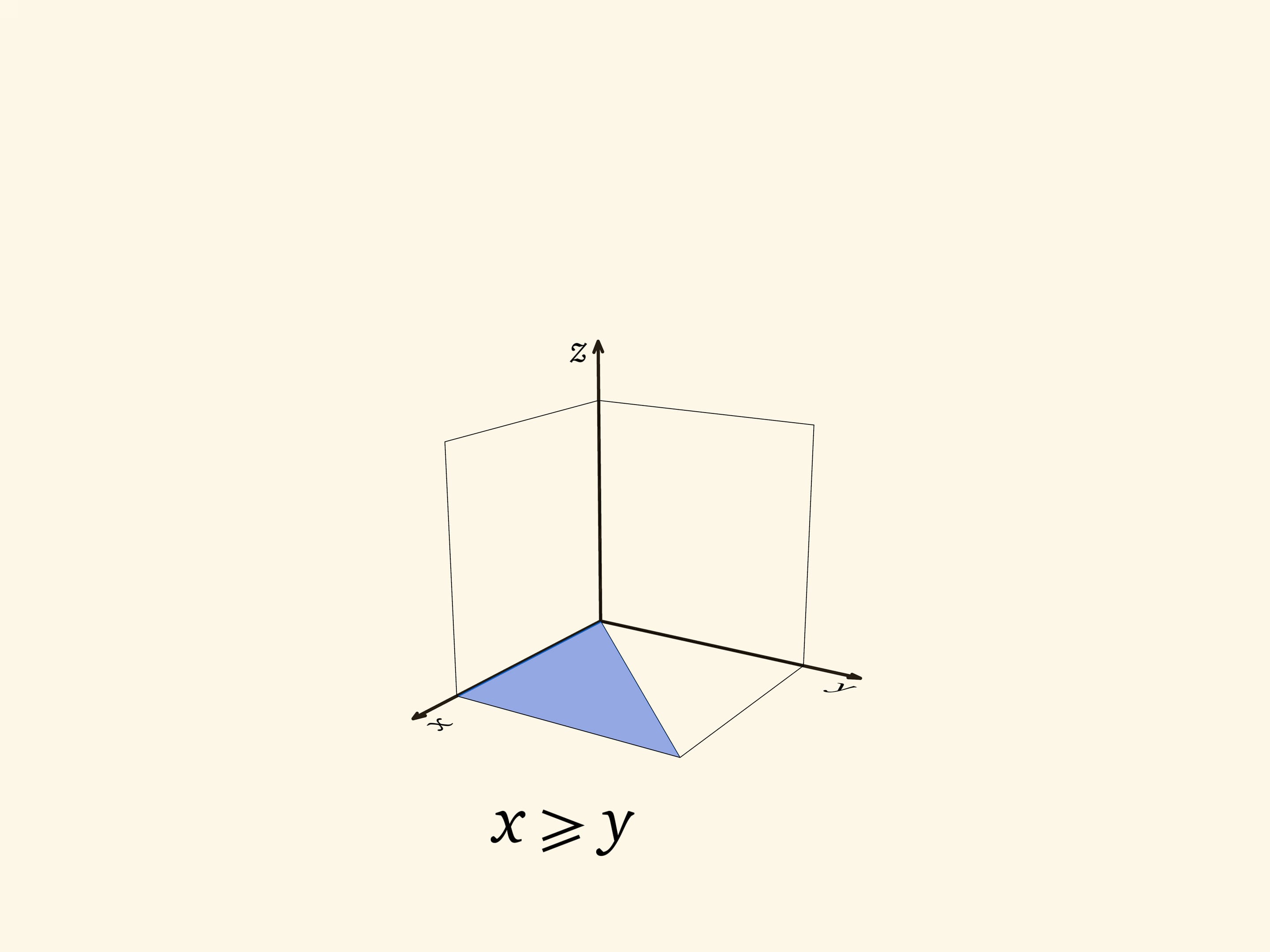
Начнём с плоского случая: не с куба, а с квадрата. На плоскости $Oxy$ квадрат с вершиной в начале координат естественным образом задаётся неравенствами $0\leqslant x\leqslant 1$, $0\leqslant y\leqslant 1$. Диагональ $x=y$ делит квадрат на две равные части: в одной части $x\geqslant y$, в другой $y\geqslant x$. Другими словами: одна половина состоит из точек $(x,y)$, у которых максимальна координата $x$, другая — из точек, у которых максимальна координата $y$.
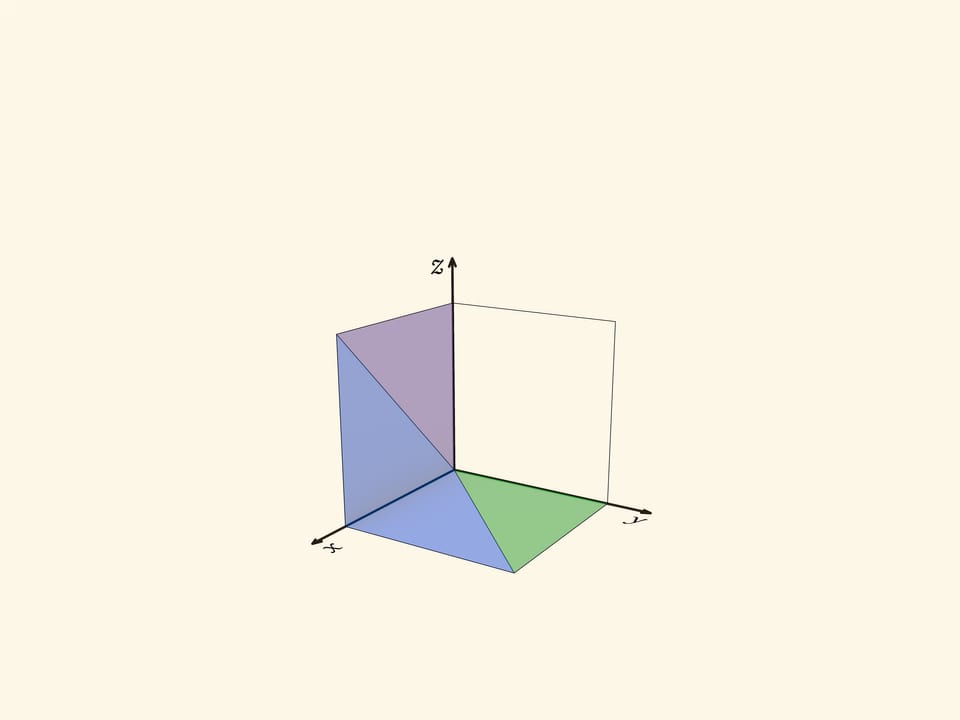
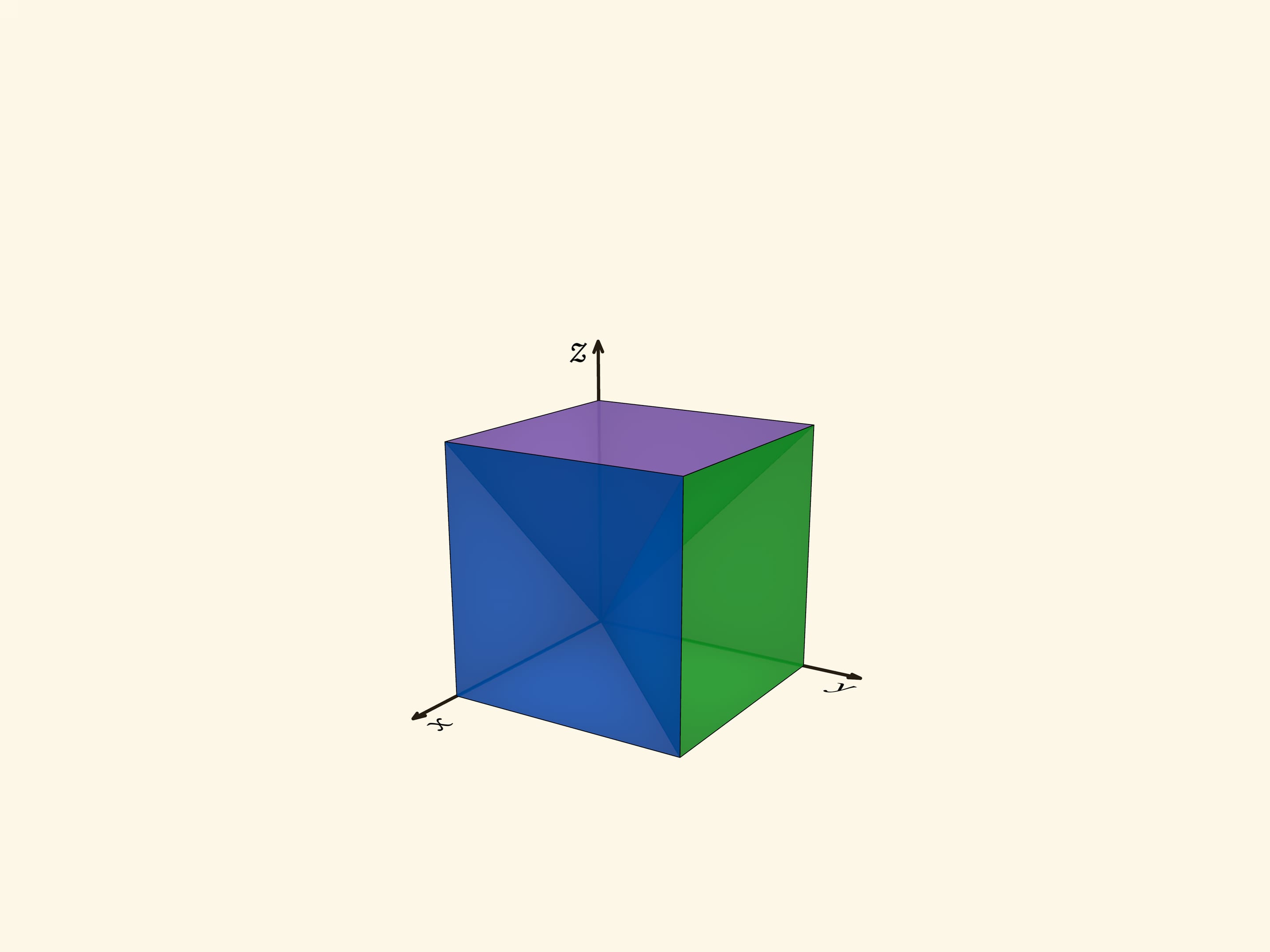
Вернёмся к кубу. Его можно задать неравенствами $0\leqslant x\leqslant 1$, $0\leqslant y\leqslant 1$, $0\leqslant z\leqslant 1$. На квадратных гранях $x=0$, $y=0$, $z=0$ возникает разбиение на две части, описанное выше.
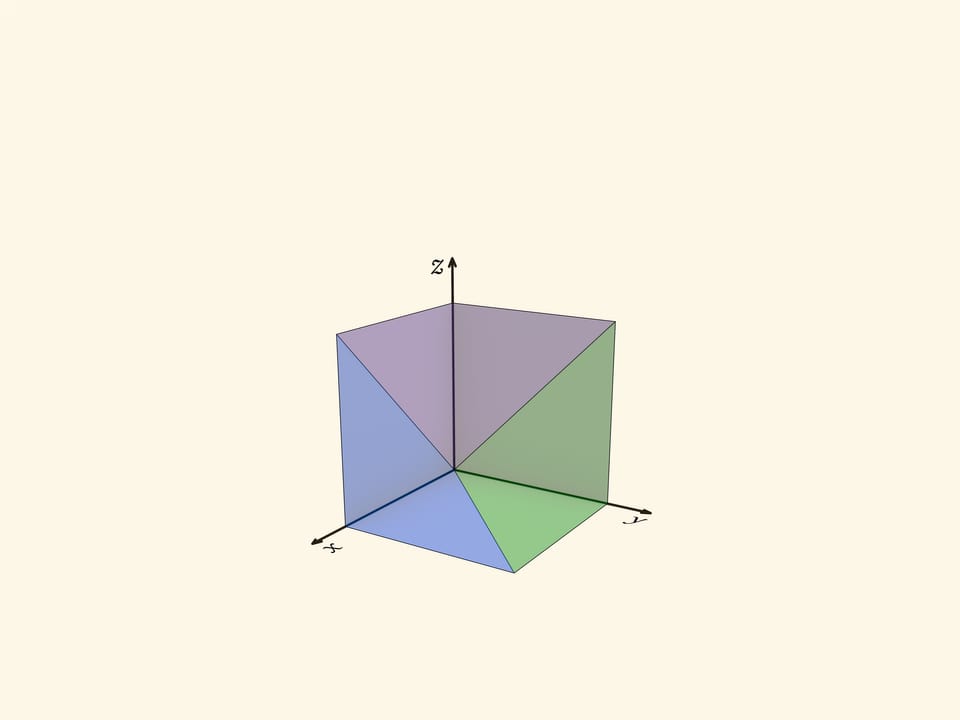
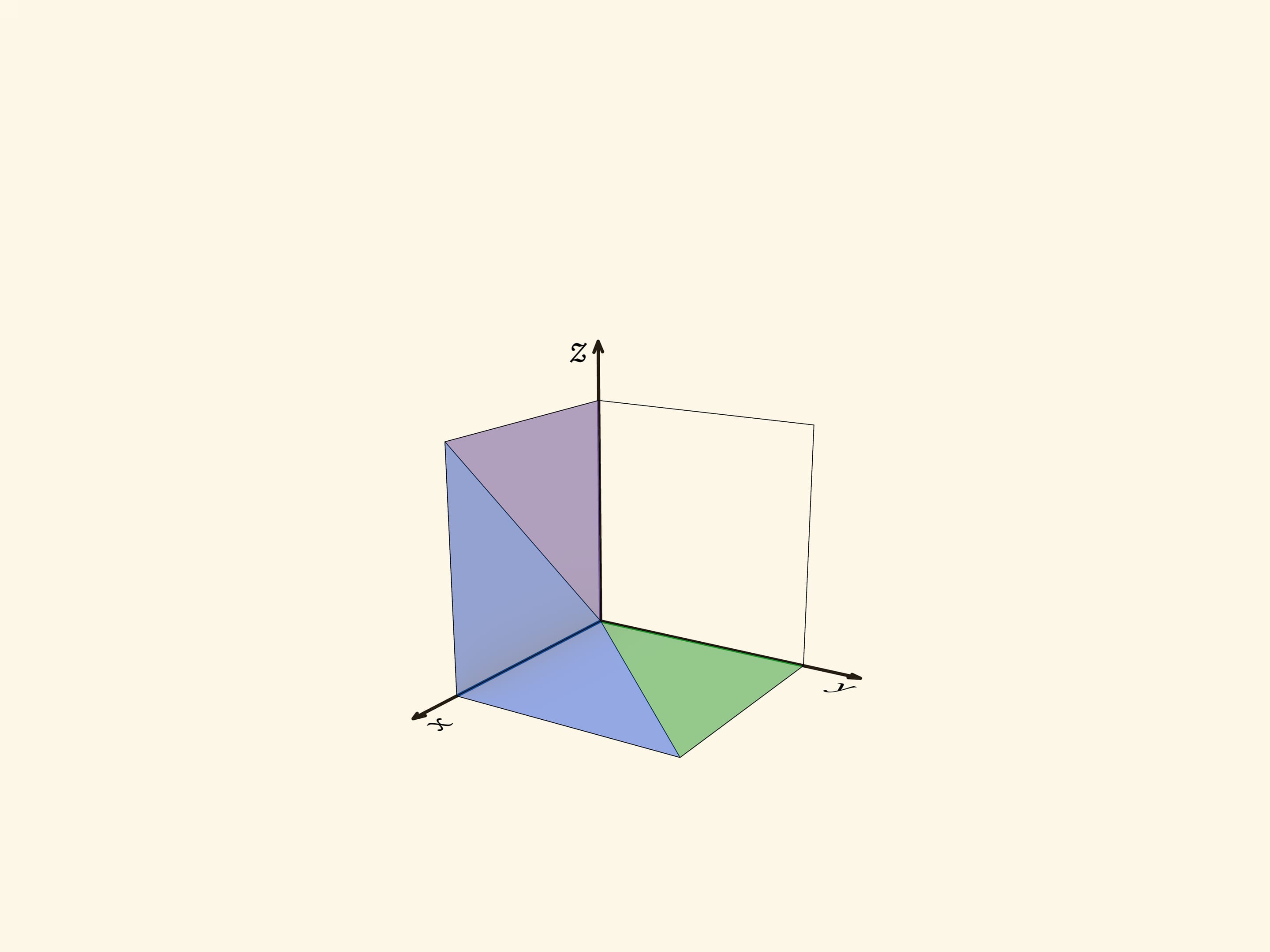
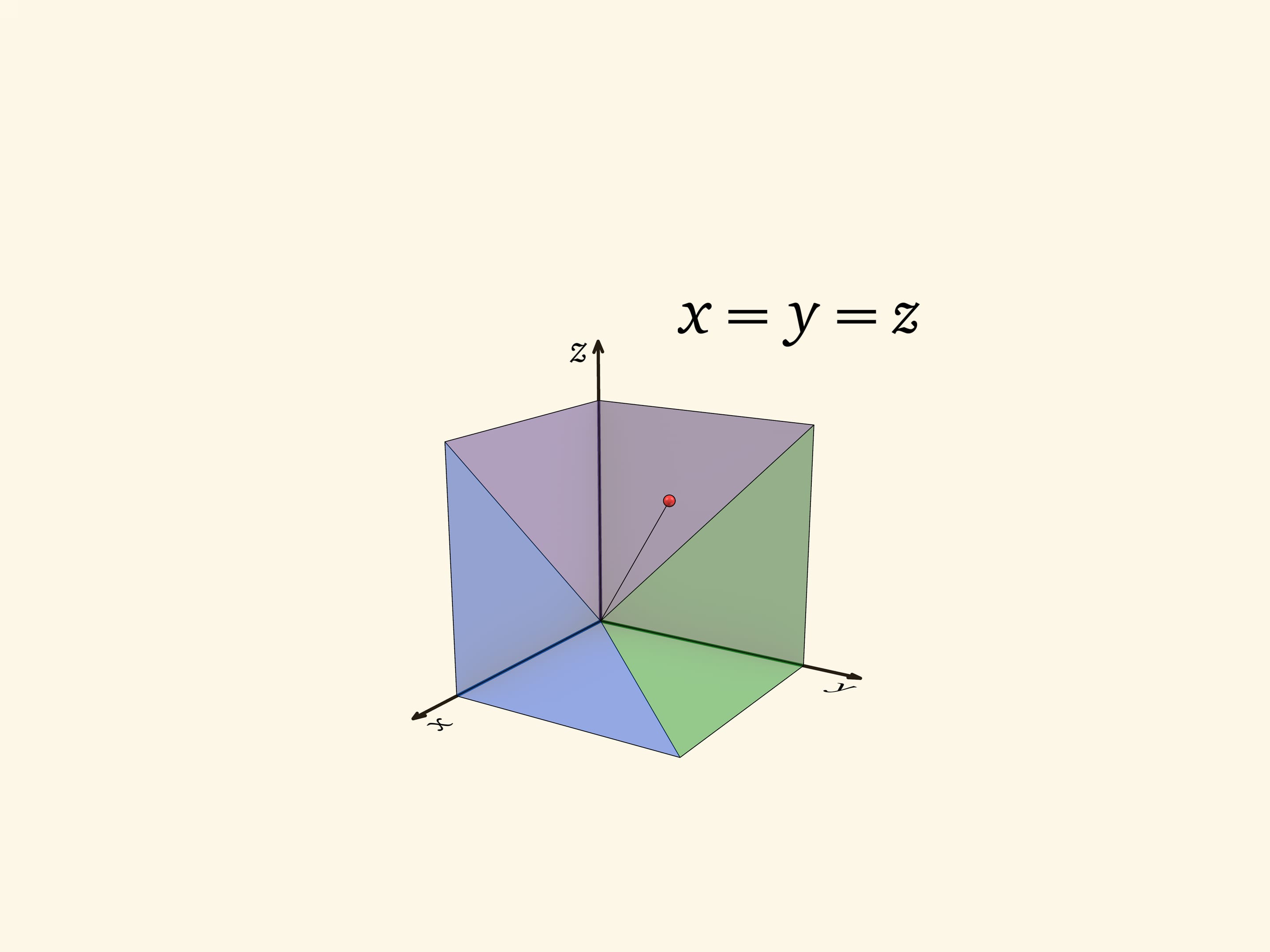
Три пирамиды, на которые геометрически разбит куб, соответствуют областям, где максимальна одна из координат, $x$, $y$ или $z$. Посмотрим на область, где максимальна координата $z$. В сечении $z=c$ этому условию отвечает квадрат $0\leqslant x\leqslant c$, $0\leqslant y\leqslant c$. Из таких сечений при разных $c$ образуется пирамида с квадратным основанием и вершиной в точке $(0,0,0)$. Две другие пирамиды получаются из рассмотренной перестановкой координат, т. е. поворотом трёхмерного пространства вокруг диагонали куба $x=y=z$. При повороте вокруг диагонали на $120^\circ$ куб переходит в себя, а пирамиды — друг в друга.
Такое симметричное задание ещё раз говорит о том, что получающиеся пирамиды одинаковы, равны.
Вытянем куб по одной из координат. Теперь уже пирамиды становятся не все равными, но при этом продолжают иметь одинаковый объём, т. е. остаются равновеликими.
Вытянем куб ещё по одному направлению — получится прямоугольный параллелепипед со всеми тремя не равными измерениями. Все три пирамиды уже не равны, но по-прежнему равновелики.
Продемонстрируем равновеликость пирамид на этом случае. Рассмотрим пирамиду, состоящую из прилегающих друг к другу половинок синей и зелёной пирамид. Их объединение — пирамида с прямоугольным основанием. Основание и любое сечение, параллельное основанию, делится общей гранью пирамид — диагональю — на две равные части. Значит, и объёмы их равны. Заметим ещё, что рассматриваемая пирамида симметрична фиолетовой пирамиде.
Скосим параллелепипед. И в этом случае можно доказать, что все три пирамиды будут иметь одинаковый объём.
В заключение напомним, что модель из трёх одинаковых пирамидок, из которых можно собрать куб, — полезна в кабинетах математики.