Задача «разрезать квадрат на квадраты» — тривиальная. Разделим стороны исходного квадрата пополам и получится разрезание на четыре одинаковых квадрата. Но если в задаче добавить условие, что все квадраты, на которые разрезается исходный квадрат, должны быть разными, то задача становится совсем не простой.
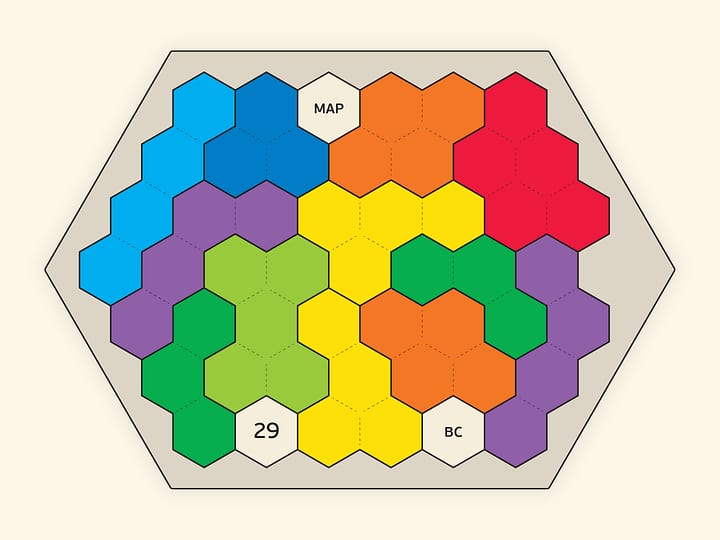
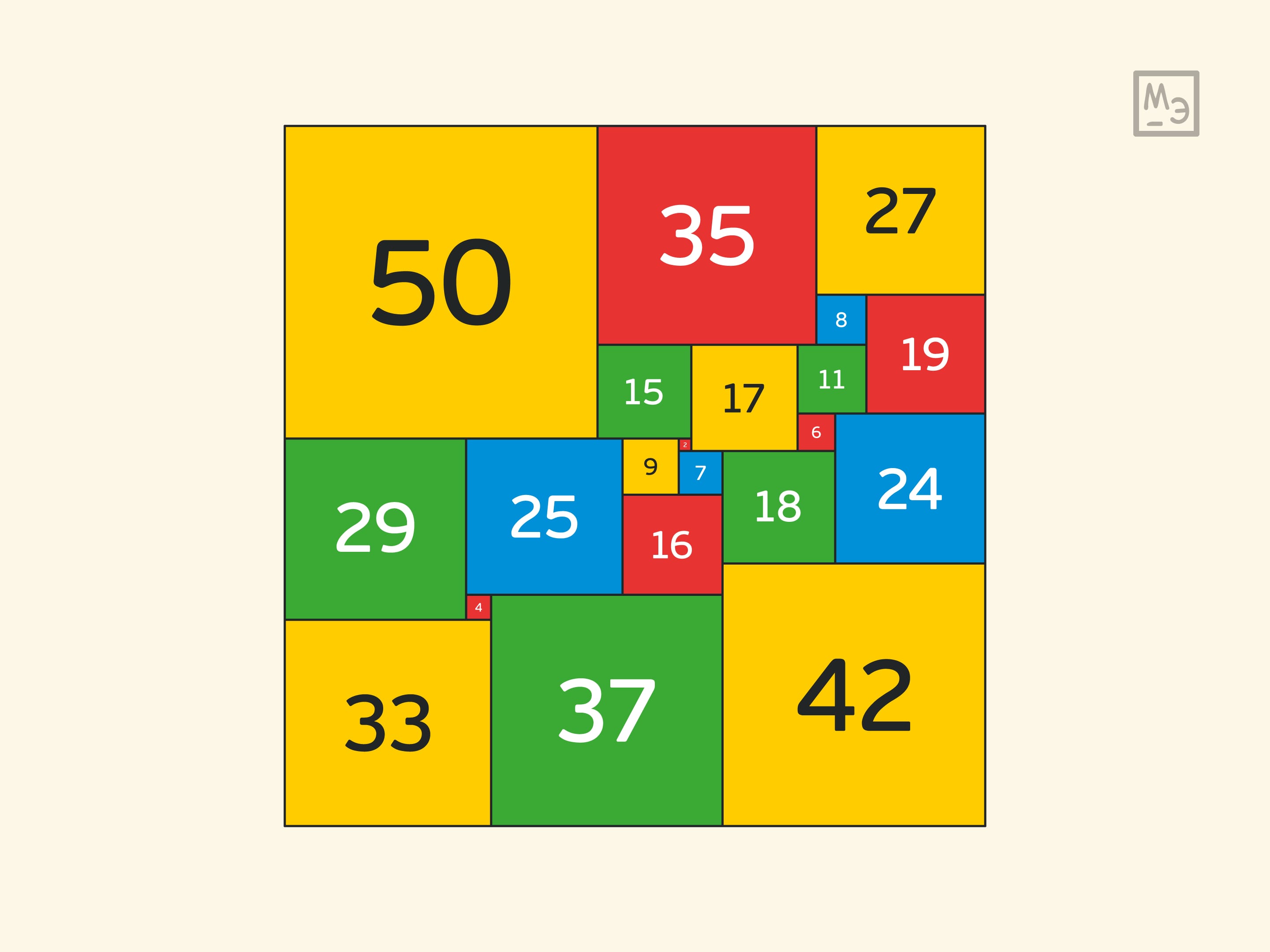
Наименьшее возможное число, на которое можно разрезать квадрат на квадраты так, чтобы они все были попарно неравными между собой, — $21$. При этом такое разбиение единственно, оно представлено на картинке.
Реализовать это разбиение в виде головоломки довольно сложно — слишком разные у этих квадратов стороны. А в виде лоскутного одеяла, скатерти или интарсии на столе — очень интересно! Но если немного «пошевелить» условие задачи, то можно сделать и нетривиальные головоломки.
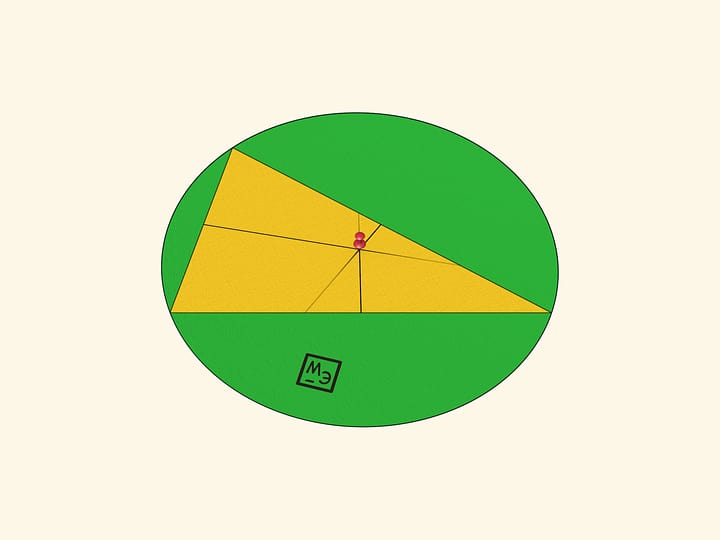
Например, разрешить не всем квадратам быть попарно различными. В приведённом примере большой фиолетовый квадрат имеет сторону $5$, два синих — $4$, зелёный — $3$, жёлтые — по $2$, а у красных квадратов сторона равна $1$.
Задачу разрезания на квадраты разумно ставить и для прямоугольника. И такая постановка имеет и историческое значение: в $1903$ году Макс Ден доказал, что если прямоугольник можно разрезать на квадраты (не обязательно равные), то отношение длин его сторон рационально.
В приведённом примере прямоугольник $32\times 33$ разделён на попарно различные квадраты (со сторонами $18$, $15$, $14$, $10$, $9$, $8$, $7$, $4$ и квадратик со стороной $1$, который при изготовлении модели следует оставить как пустое место, оговорив это в описании).
Красота этих головоломок в том, что они могут стать введением в интересную область на стыке математики и физики. Ведь найденный способ решения задачи о квадрировании квадрата (или прямоугольника) основывается на правилах Кирхгофа из теории электрических цепей!
Литература
Яглом И. М. Как разрезать квадрат?. — М.: Наука, 1968. — (Математическая библиотечка). — [Возможность разбиения на 21 квадрат ещё не была известна!].
Гарднер М. Математические головоломки и развлечения. — М.: Мир, 1999. — [Глава «Квадрирование квадрата»].
Скопенков М., Прасолов М., Дориченко С. Разрезания металлического прямоугольника // Журнал «Квант». — 2011. — № 3. — Стр. 10—16.