Обратная теорема Пифагора ⁠

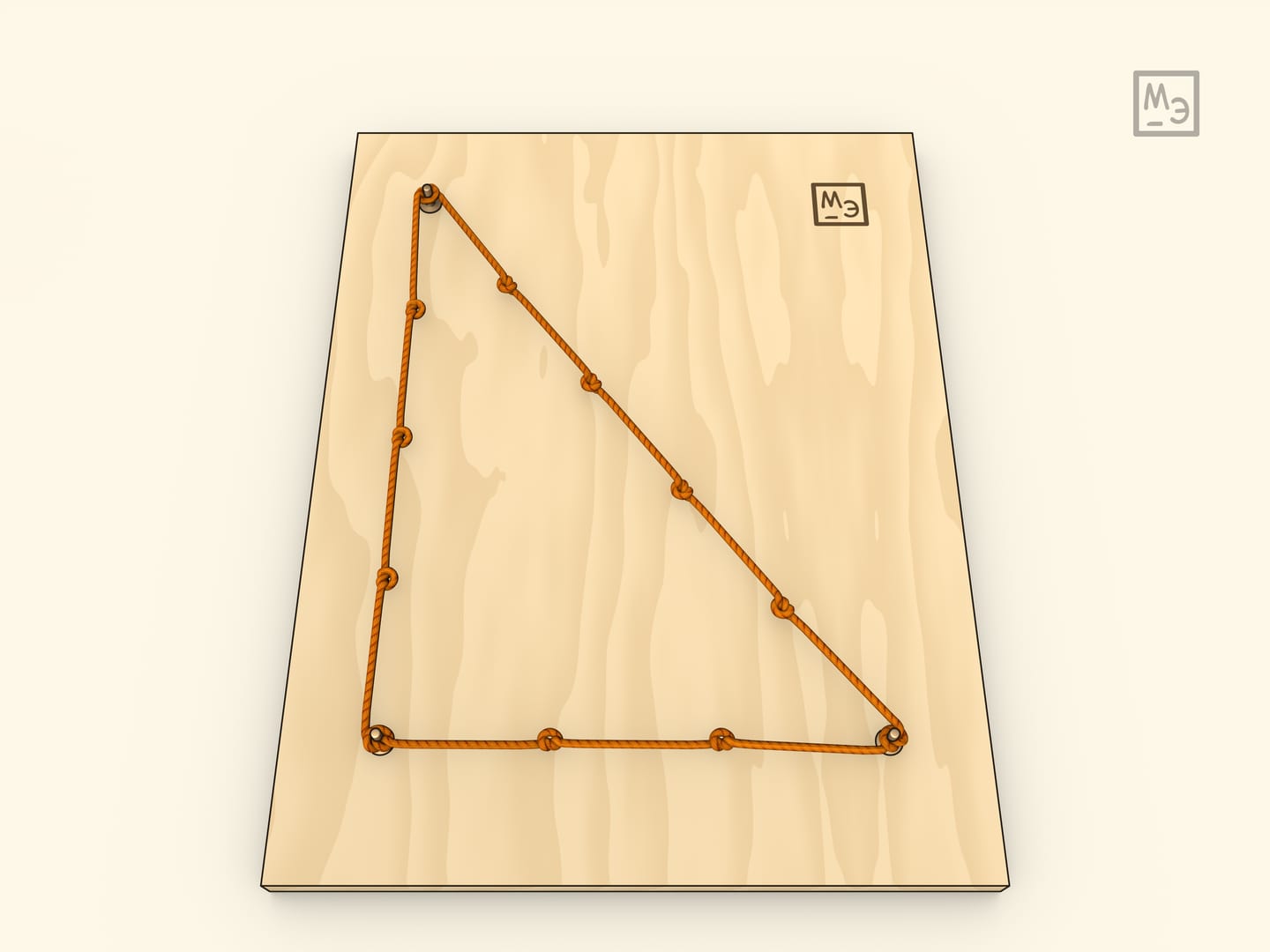
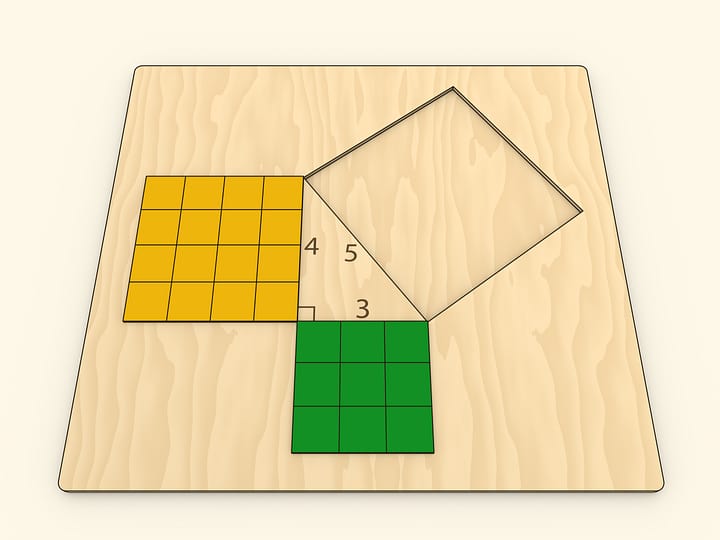
Если в тре­уголь­нике сумма квад­ра­тов длин двух сто­рон равна квад­рату длины тре­тьей сто­роны, то тре­уголь­ник — прямо­уголь­ный. Таким обра­зом, если для трёх положи­тель­ных чисел выпол­нено равен­ство $a^2+b^2=c^2$, то суще­ствует прямо­уголь­ный тре­уголь­ник с кате­тами $a$, $b$ и гипо­те­ну­зой ${c}$. Обрат­ная тео­рема Пифагора завершает книгу первую «Начал» Евклида (пред­ложе­ние XLVIII).

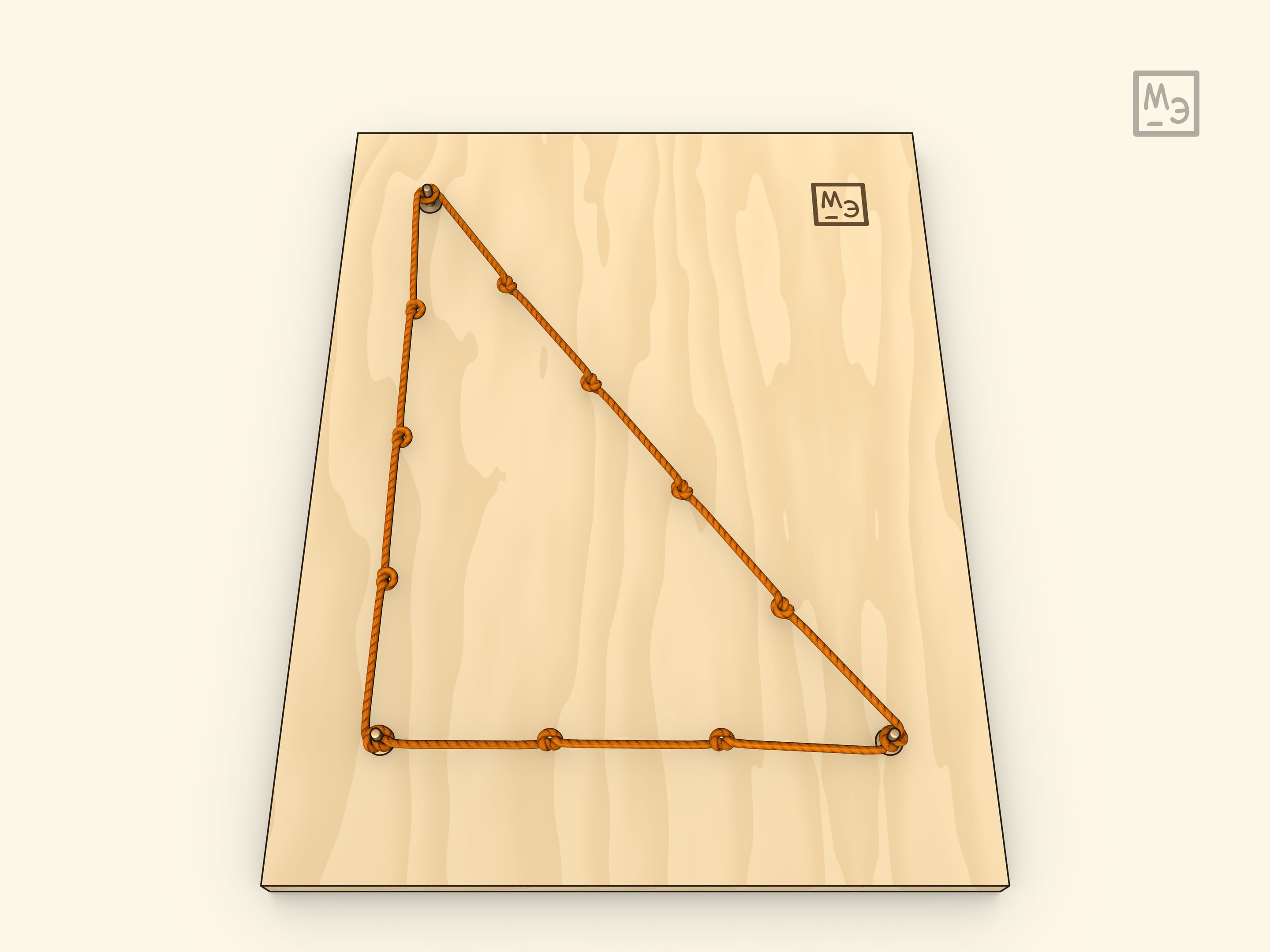
Счи­та­ется, что в Древ­нем Египте обрат­ную тео­рему Пифагора исполь­зо­вали для постро­е­ния прямого угла: завя­зы­вали на верёвке через рав­ные рас­сто­я­ния $12$ узел­ков и стро­или тре­уголь­ник $3:4:5$. Люди, обла­дающие этим зна­нием, были обра­зо­ван­ными, зача­стую рабо­тали пис­цами, но назы­вали их «гарпе­до­напт» — «натяги­вающий верёвку».

Сохра­ни­лась и расшиф­ро­вана древ­не­ва­ви­лон­ская гли­ня­ная таб­личка Plimpton 322 (XIX—XVII вв. до н. э.). Кли­нопис­ный текст содержит пере­чис­ле­ние нескольких прямо­уголь­ных тре­уголь­ни­ков: цело­чис­лен­ные длины сто­рон; вели­чины, обрат­ные квад­ра­там синуса одного из углов.