Правильный пятиугольник: узел из полоски бумаги ⁠

Пра­виль­ный пяти­уголь­ник можно постро­ить с помощью цир­куля и линейки. Один из алго­ритмов при­ве­дён в «Нача­лах» Евклида. А можно постро­ить за минуту и без цир­куля, и без линейки!

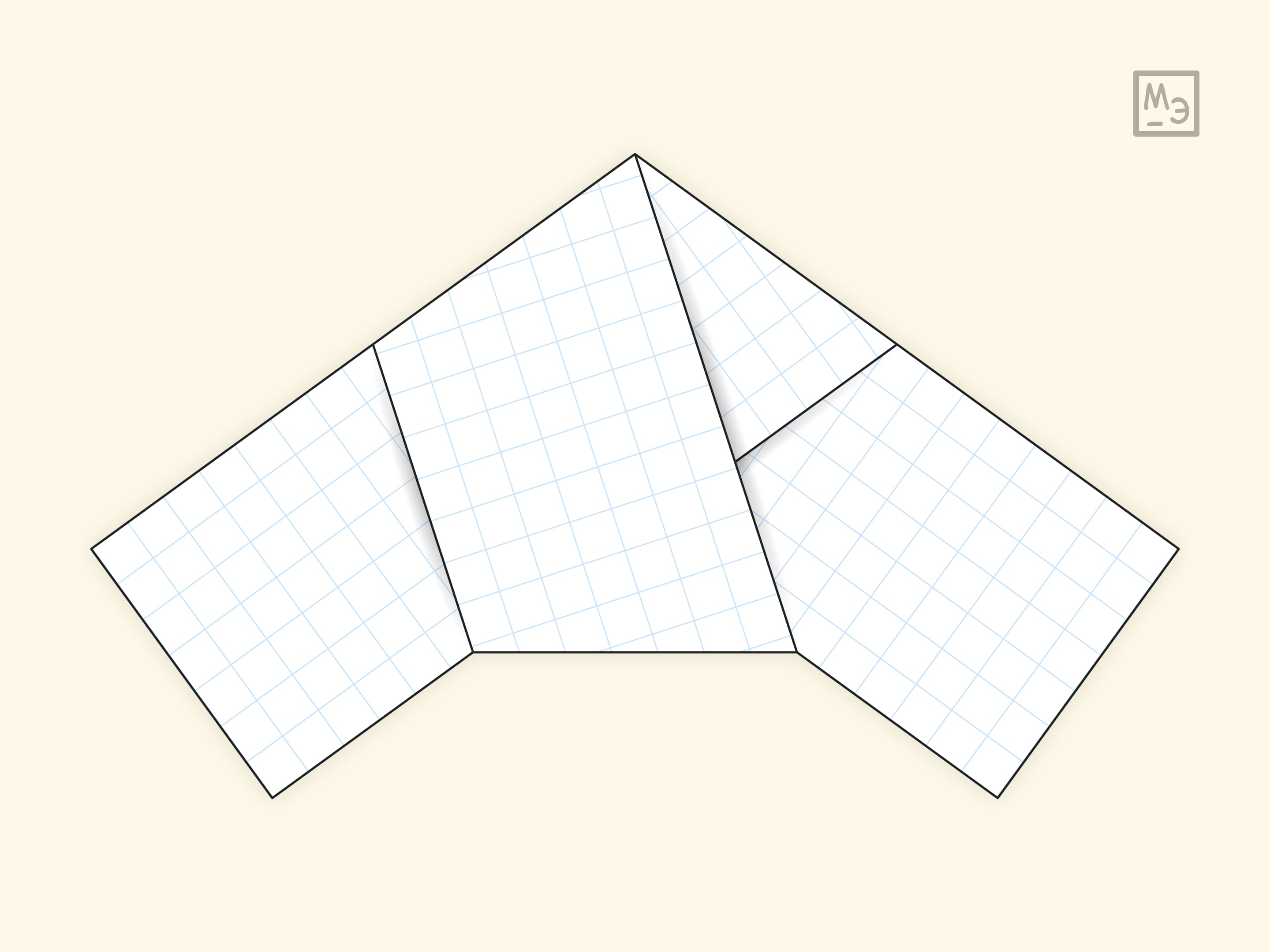
Отрежьте полоску бумаги и, не затяги­вая, завяжите её узлом. Акку­ратно затя­ните узел так, чтобы полоска не скру­чи­ва­лась, а сам узел стал плос­ким. Полу­чится пра­виль­ный пяти­уголь­ник! При жела­нии можно обре­зать и загнуть «хво­стики».

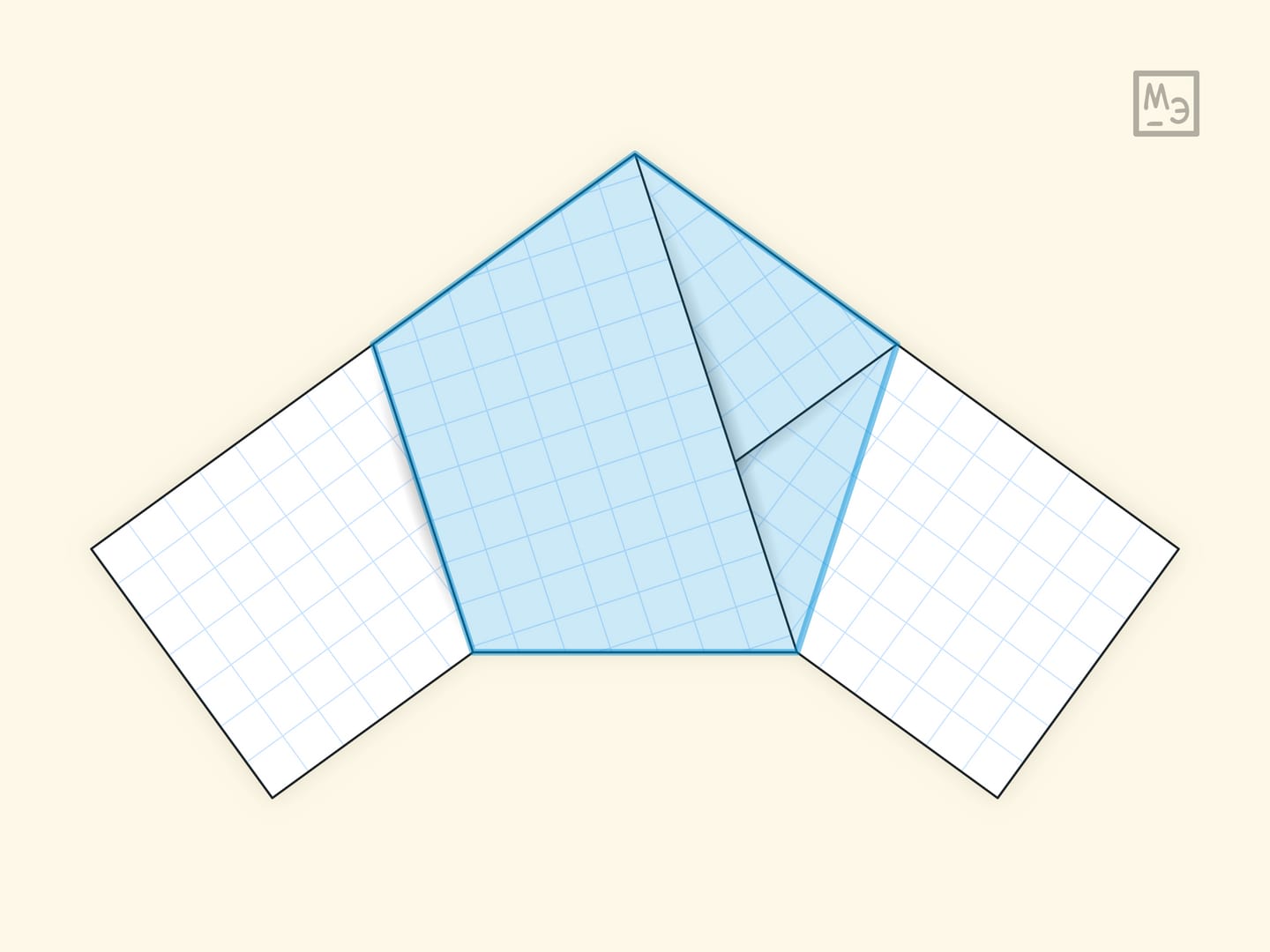
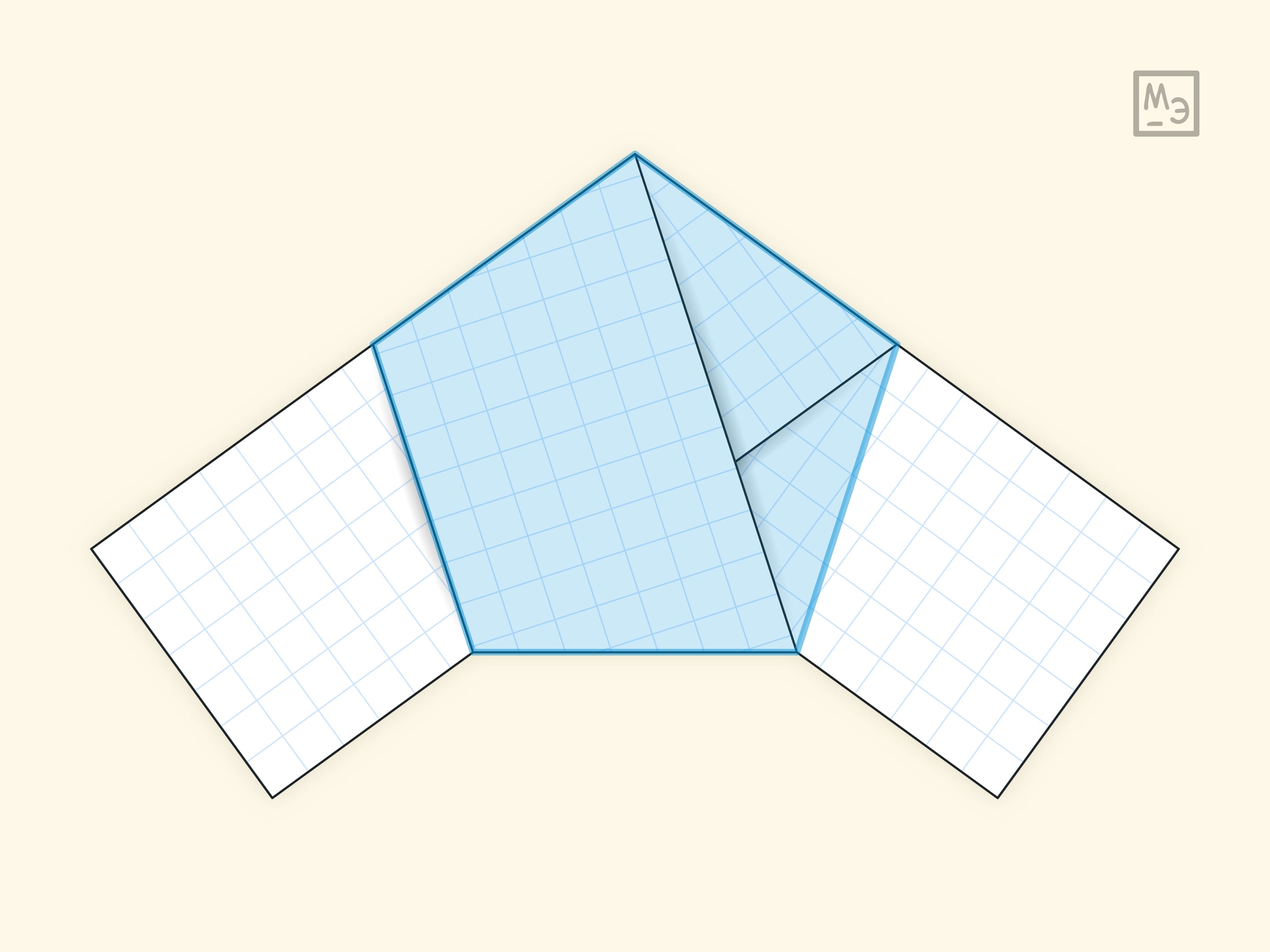
Попро­буйте само­сто­я­тельно дока­зать, что полу­чен­ная фигура — пра­виль­ный пяти­уголь­ник. Под­сказ­кой может служить всё та же полоска бумаги: если узел раз­вер­нуть, то будут видны трапе­ции, у кото­рых одно осно­ва­ние — сто­рона пяти­уголь­ника, а другое осно­ва­ние — его диаго­наль.

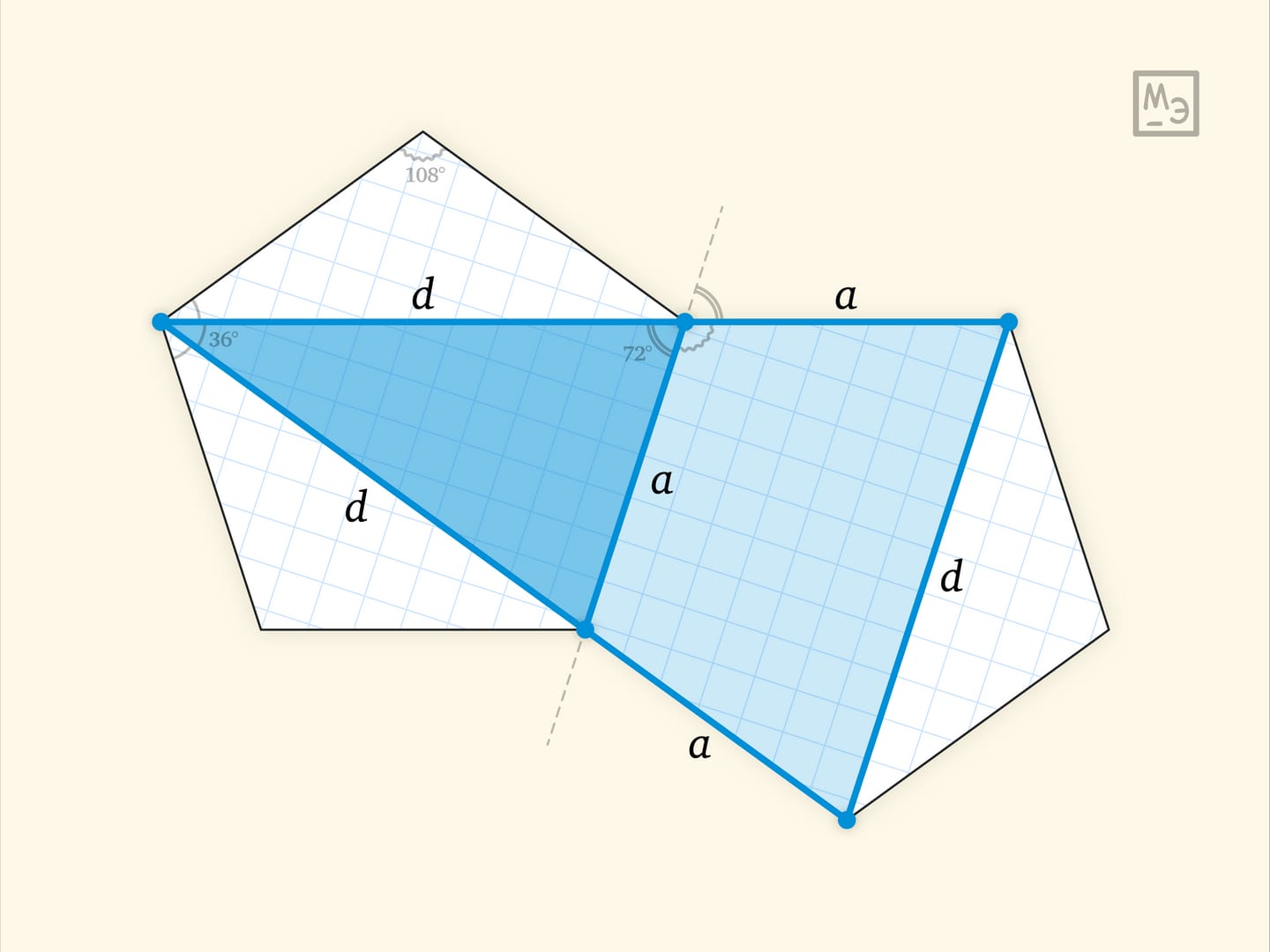
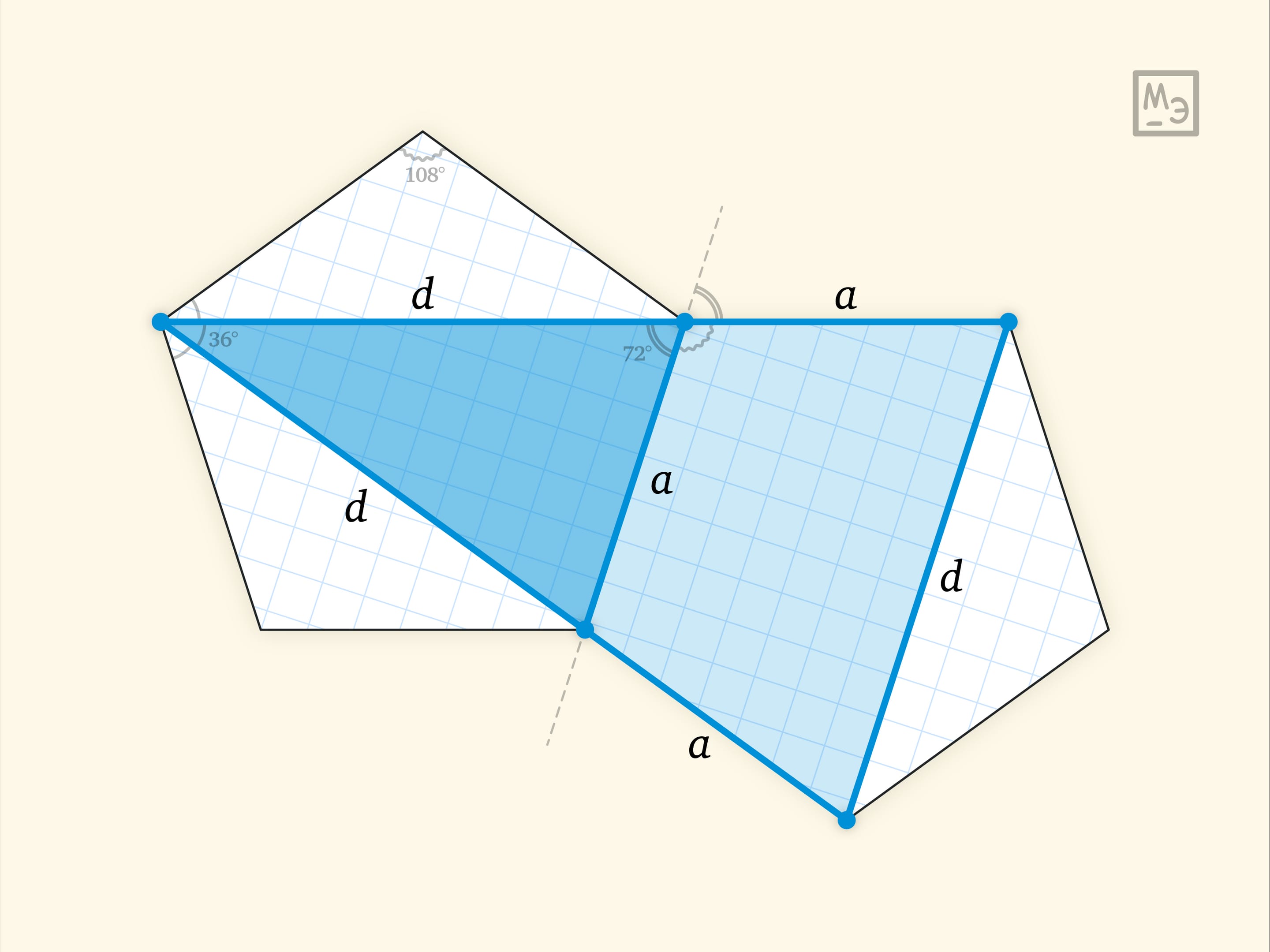
Обо­зна­чим длину сто­роны пра­виль­ного пяти­уголь­ника $a$, а длину его диаго­нали $d$. Отра­зим пра­виль­ный пяти­уголь­ник отно­си­тельно сто­роны. Сто­рона пяти­уголь­ника-образа и диаго­наль исход­ного лежат на одной прямой: в этом можно убе­диться, посчи­тав углы.

Из подо­бия синих тре­уголь­ни­ков сле­дует про­порция $\frac{d}{a}=\frac{d+a}{d}$. Пере­множив крест-накрест, полу­чаем важ­ное соот­ноше­ние между элемен­тами пра­виль­ного пяти­уголь­ника: $a^2+ad=d^2$. Из него несложно выве­сти, что отноше­ние диаго­нали пра­виль­ного пяти­уголь­ника к сто­роне равно золо­тому сече­нию: $\frac da=\frac{1+\sqrt5}2$. (Тем самым, у нас есть два параметра, отноше­ние кото­рых выража­ется через квад­рат­ные корни. Именно это и обес­пе­чи­вает возмож­ность постро­е­ния пра­виль­ного пяти­уголь­ника цир­ку­лем и линейкой.)

Постро­е­ние пра­виль­ного пяти­уголь­ника завя­зы­ва­нием узла на полоске бумаги пере­да­ётся «из уст в уста». Это постро­е­ние можно обобщить и на другие пра­виль­ные много­уголь­ники с нечёт­ным (большим 5) чис­лом сто­рон.