Задача о диване ⁠

Насколько большой диван можно про­не­сти через кори­дор, пово­ра­чи­вающий на прямой угол? При пере­носе мебели иногда решающие сан­тиметры выга­ды­ваются вся­че­скими подъёмами и накло­нами. Матема­ти­че­ская «задача о диване», постав­лен­ная в 1966 году, рас­смат­ри­вает плос­кий (каза­лось бы, про­стой) слу­чай, но до сих пор она окон­ча­тельно не решена.

Итак, в плос­ко­сти рас­смат­ри­ва­ется кори­дор еди­нич­ной ширины, пово­ра­чи­вающийся на прямой угол. Фигуру какой мак­сималь­ной площади можно про­не­сти по такому кори­дору?

Оче­видно, что диван в виде еди­нич­ного квад­рата может «пройти» угол. Дру­гой про­стой при­мер — полу­круг ради­уса 1. Площадь такого дивана уже $\pi/2\approx 1{,}57$.

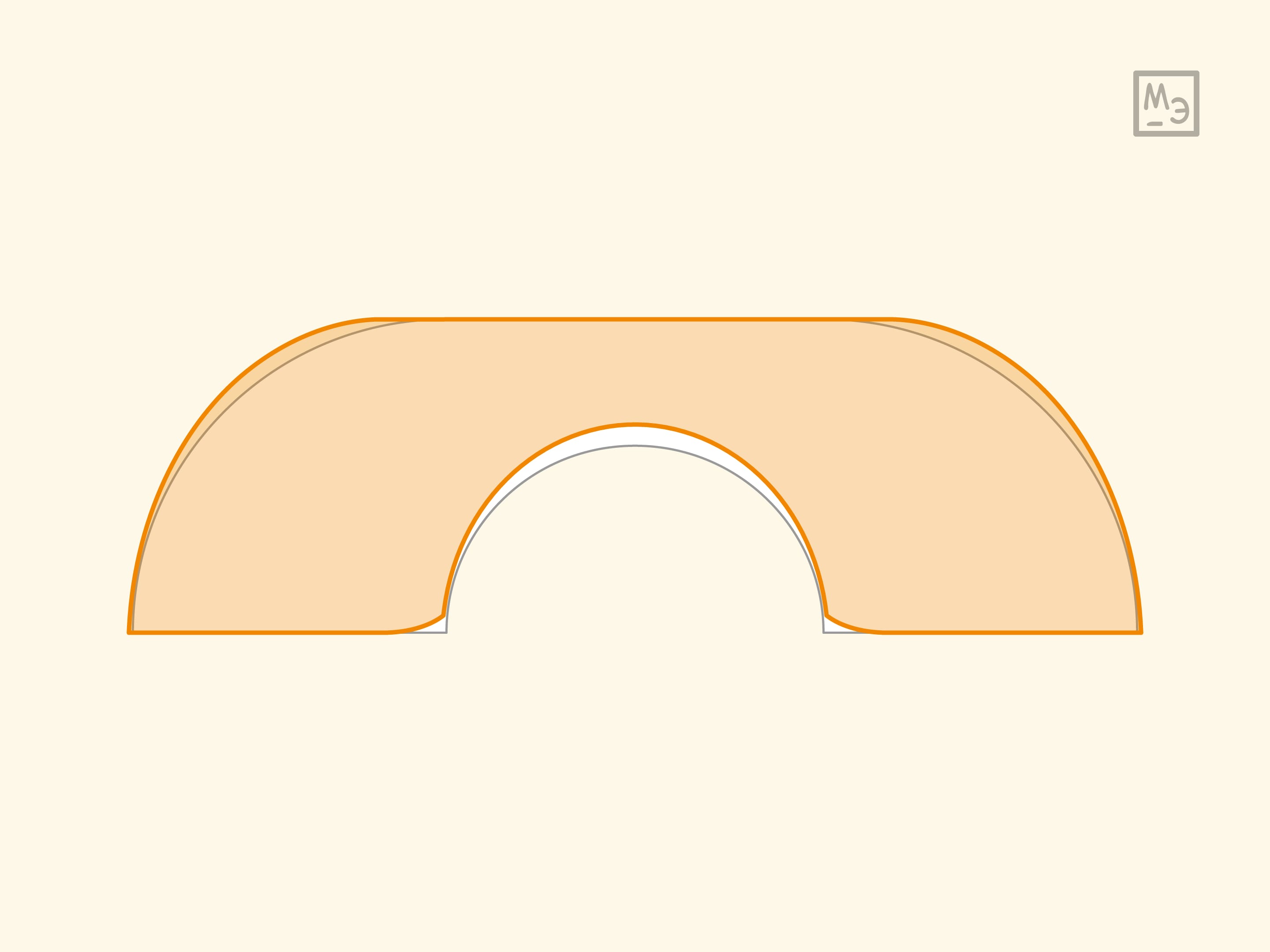
При перемеще­нии квад­рата исполь­зуются парал­лель­ные пере­носы, а для полу­круга — пово­рот. Объеди­не­ние этих движе­ний про­во­дит к кон­струкции Джона Хаммерсли: полу­круг ради­уса 1 раз­ре­за­ется на две чет­вер­тинки круга, между кото­рыми встав­ля­ется прямо­уголь­ник с выре­зан­ным полу­кругом, постро­ен­ным на большой сто­роне как на диаметре. Про­хо­дить угол такой диван может при ради­усе выре­за­емого полу­круга от 0 до 1, но мак­сималь­ная площадь дивана достига­ется при ради­усе полу­круга $2/ \pi$. Площадь такого дивана выража­ется кра­си­вым чис­лом $\pi/2 + 2/ \pi \approx 2{,}20746$, а кон­струкция довольно про­ста и могла бы пре­тен­до­вать на оптималь­ность.

Но в 1992 году Йозефом Гер­ве­ром была най­дена фигура, у кото­рой площадь чуть больше — при­мерно $2{,}2195$. Эта фигура огра­ни­чена тремя отрез­ками и 15 кри­выми, кото­рые нахо­дятся из реше­ния диффе­ренци­аль­ных урав­не­ний.

В задаче на мак­симум кон­крет­ные при­меры дают оценку снизу. Наи­лучшая на сегодня оценка сверху на площадь дивана была полу­чена в 2017 году и равна $2{,}37$. Зазор ещё оста­ётся.