Основой модели является круг, с расставленными по окружности и в центре столбиками. Дополняет его набор резиночек, лучше разноцветных, разной длины и с петельками на концах.
Существенно раньше темы вписанных углов в школьной программе изучается замечательное свойство окружности: вершины прямых углов прямоугольных треугольников с данной гипотенузой лежат на окружности, построенной на гипотенузе как на диаметре. То же самое в терминах вписанных углов: любой угол, опирающийся на диаметр, — прямой. Доказывается это проведением медианы на гипотенузу, которая разбивает изначальный треугольник на два равнобедренных.
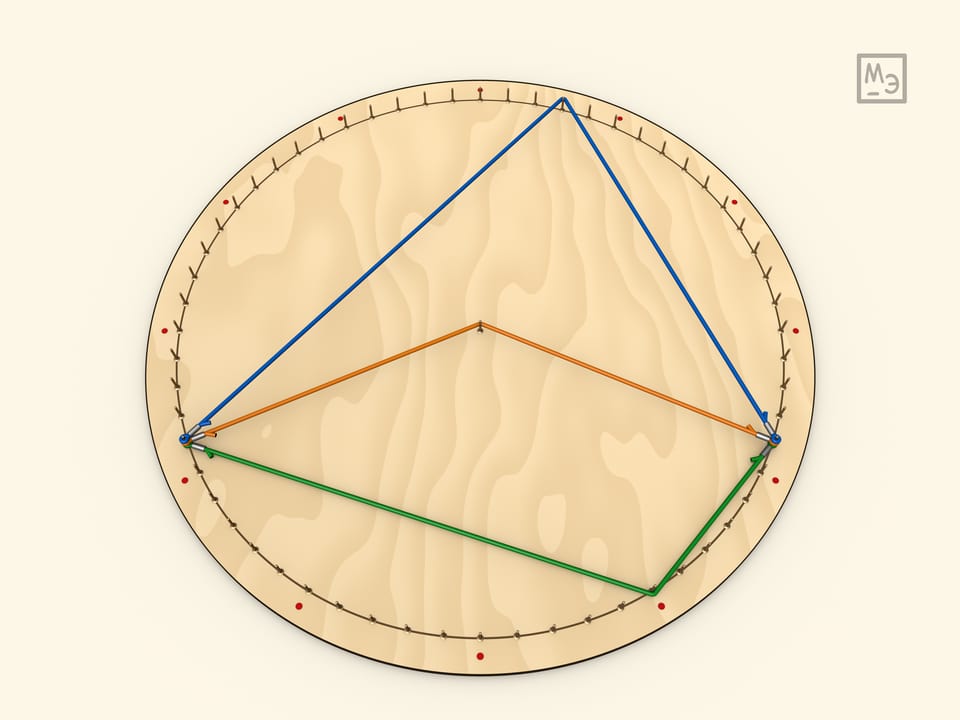
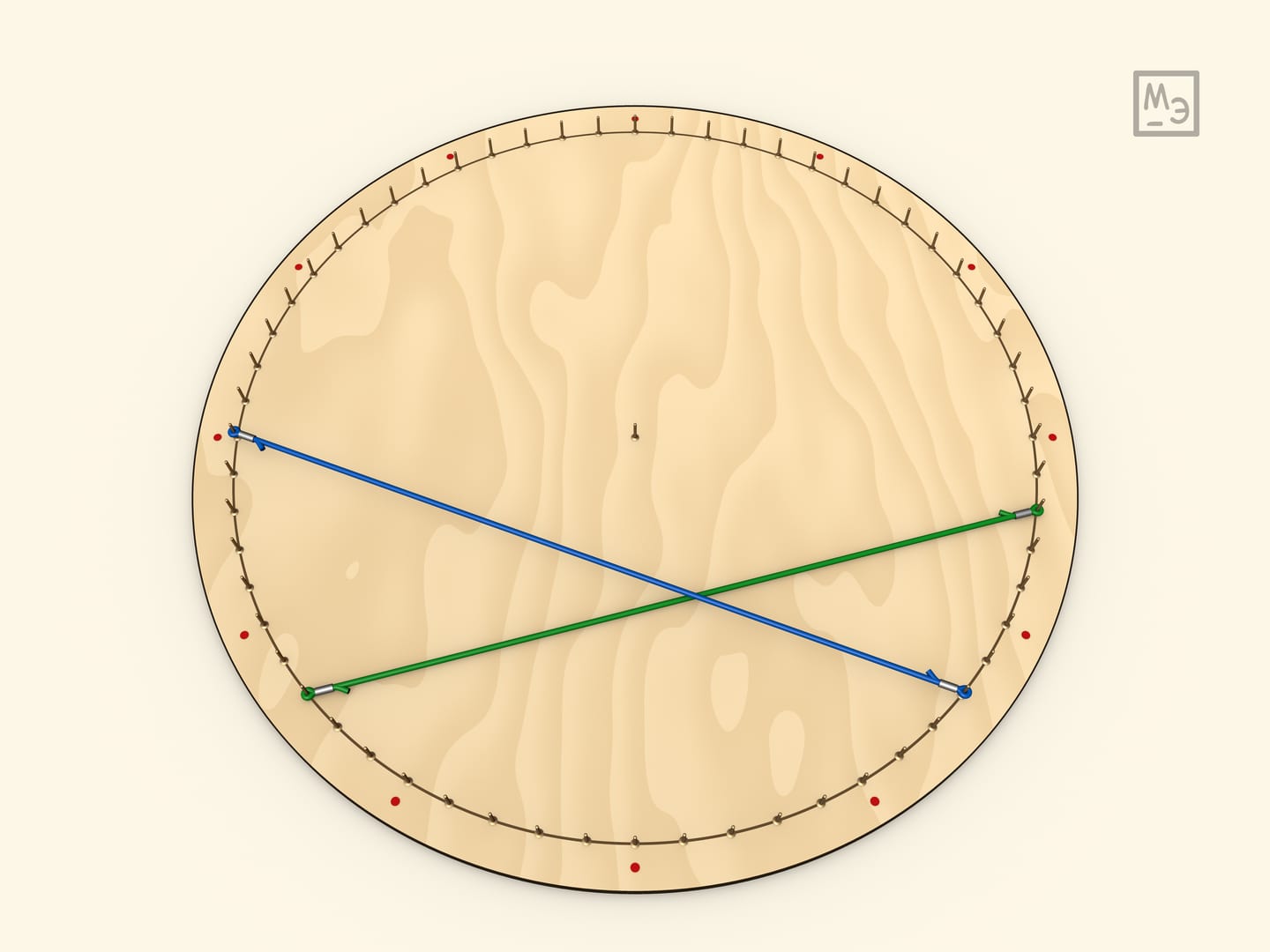
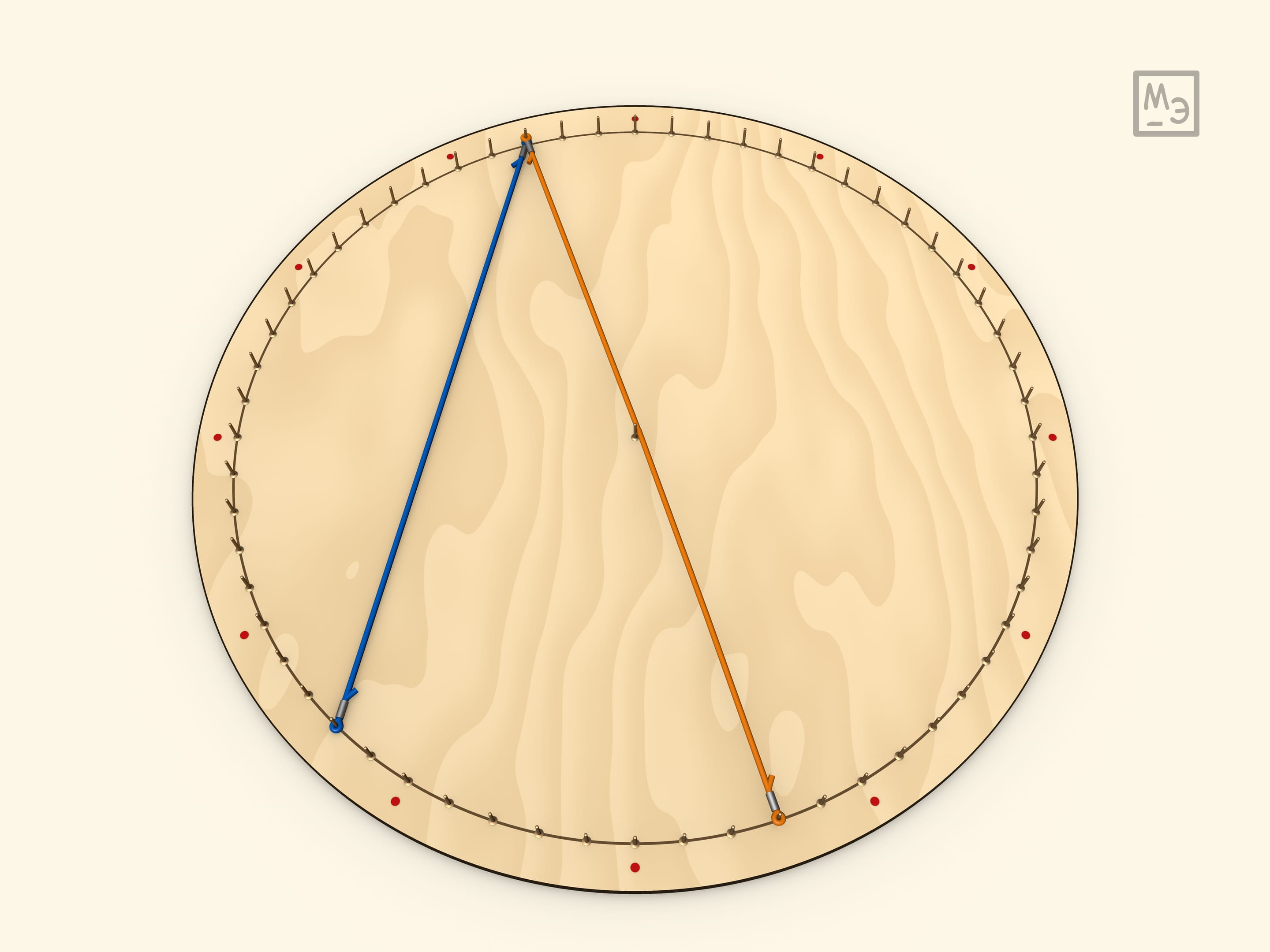
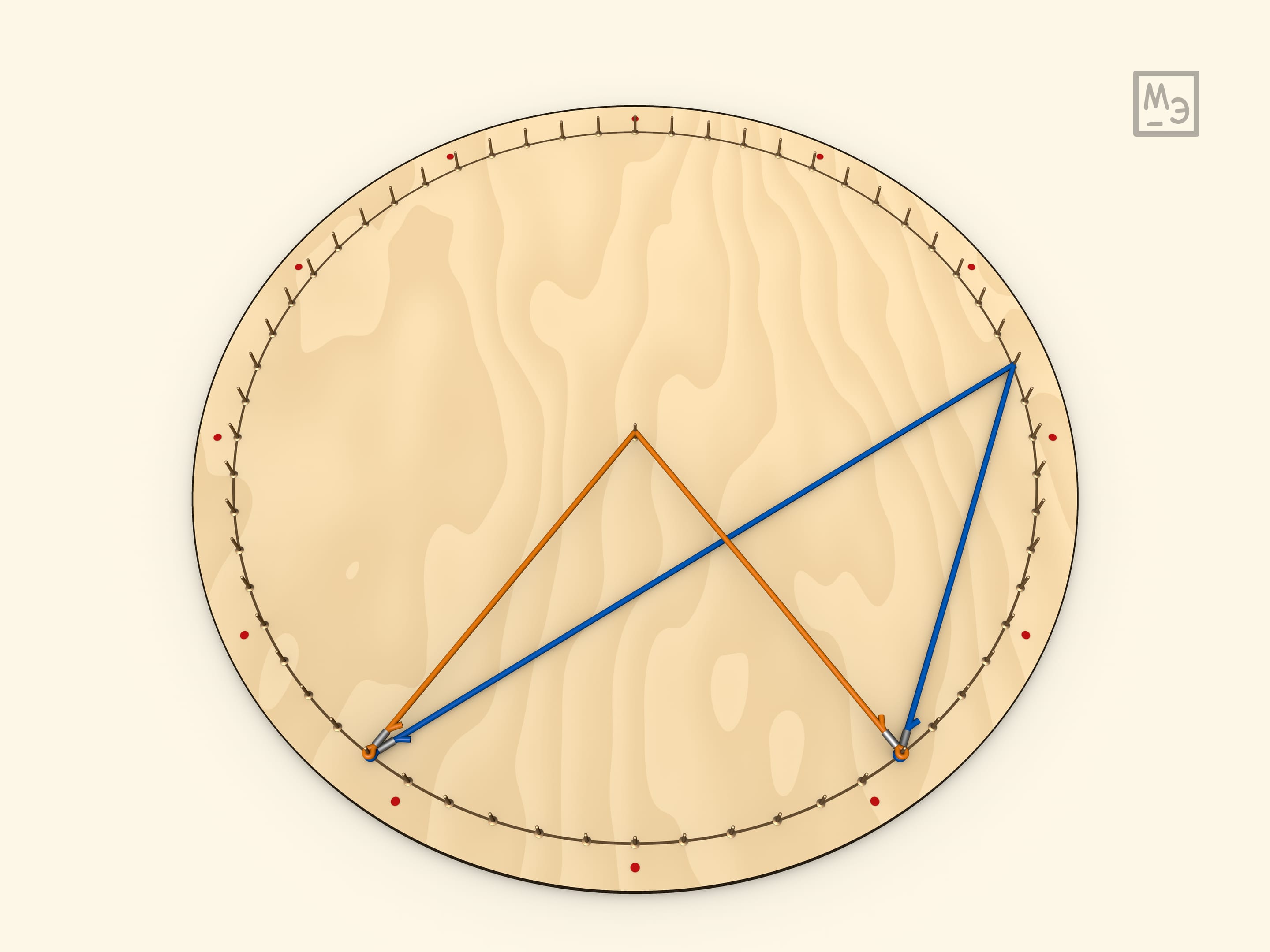
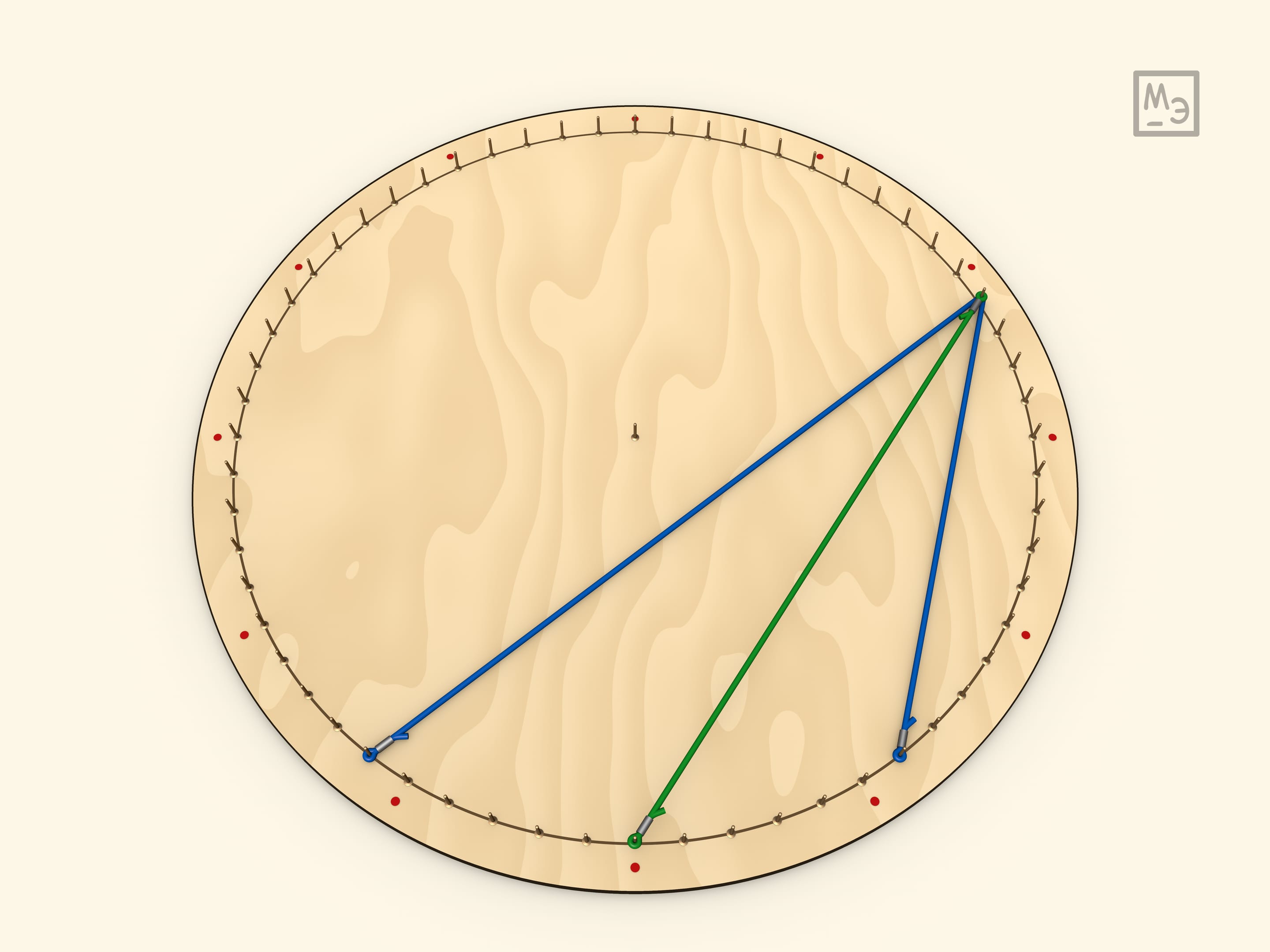
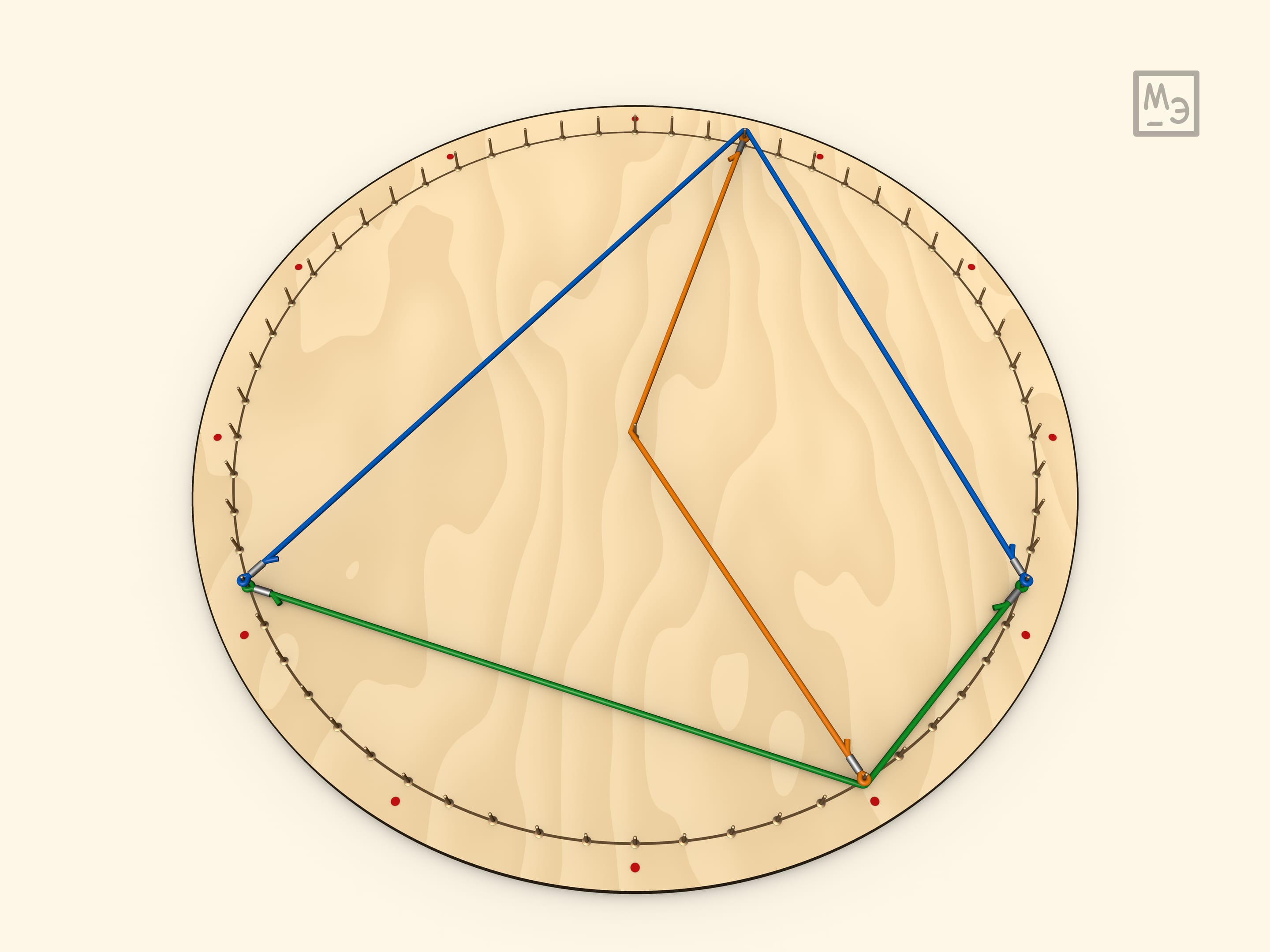
Покажем, что вписанный угол равен половине центрального.
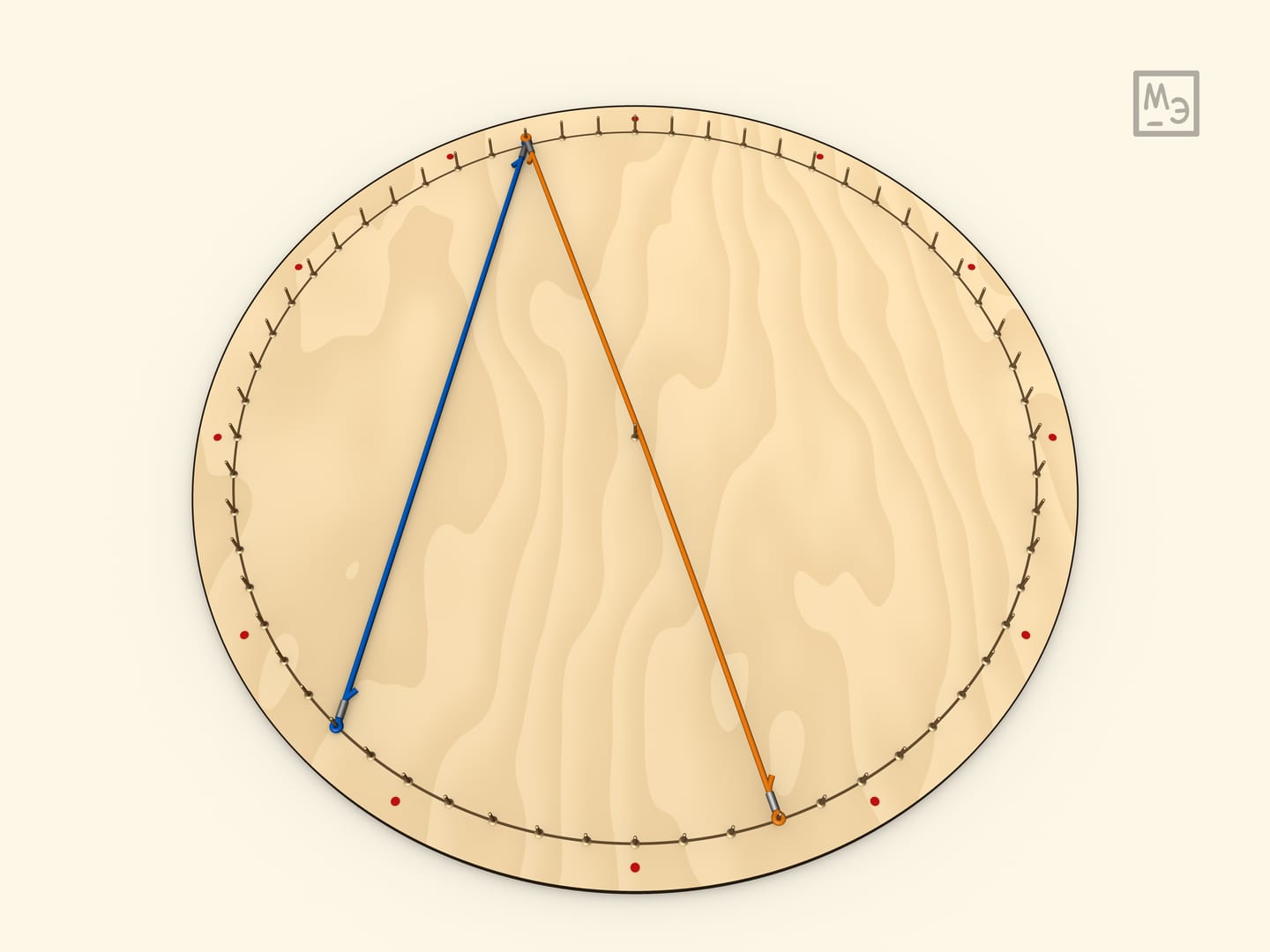
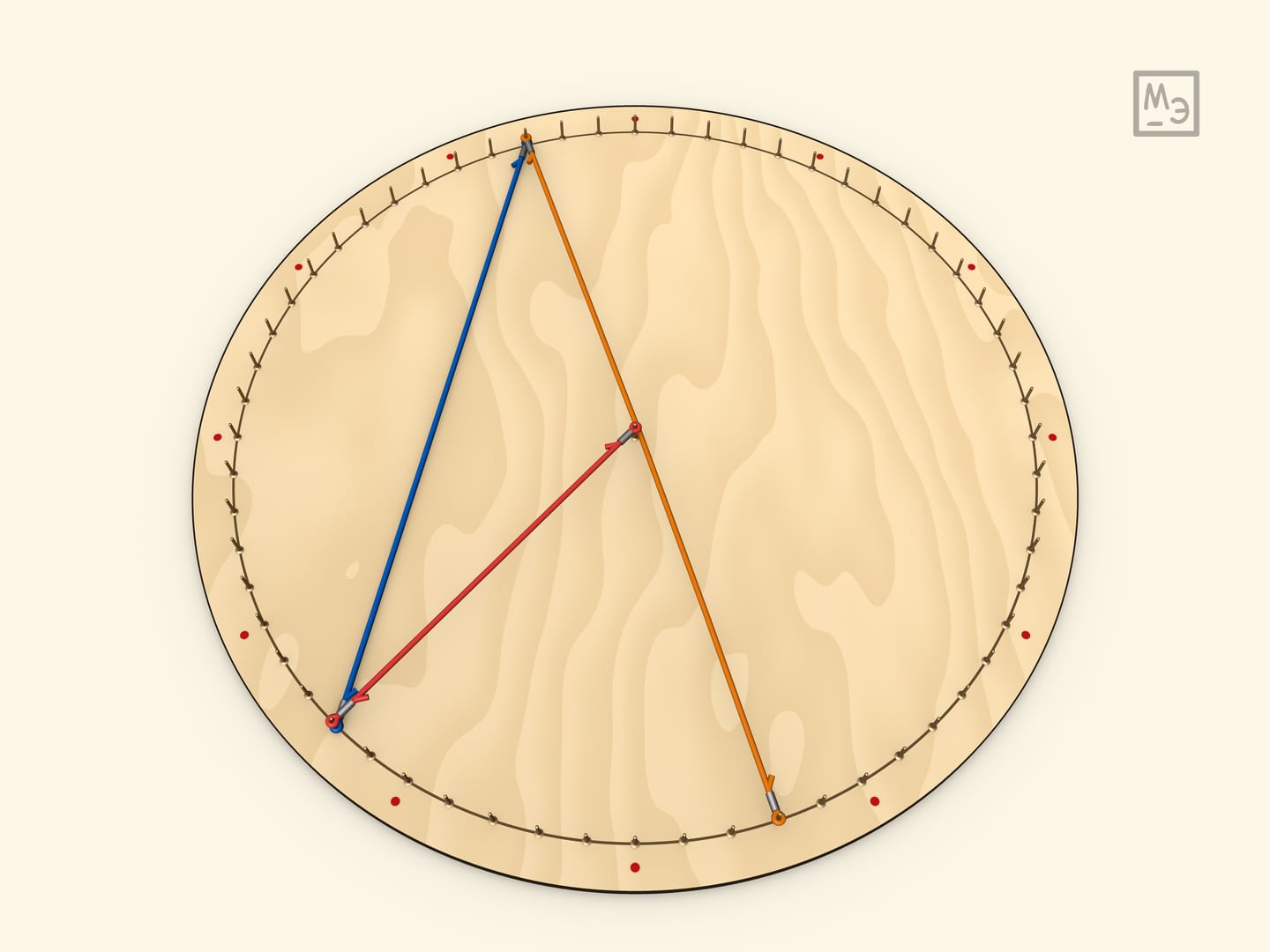
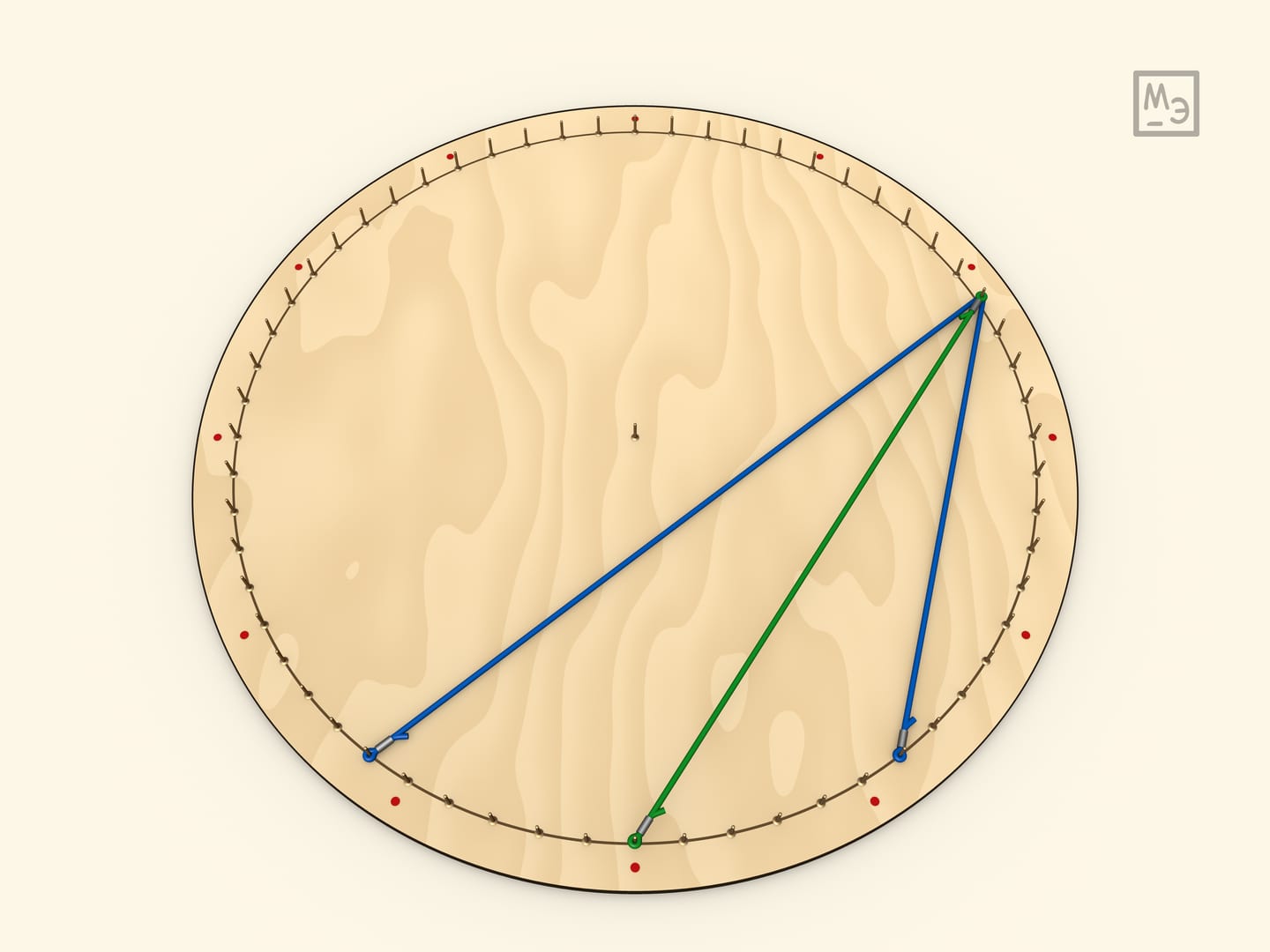
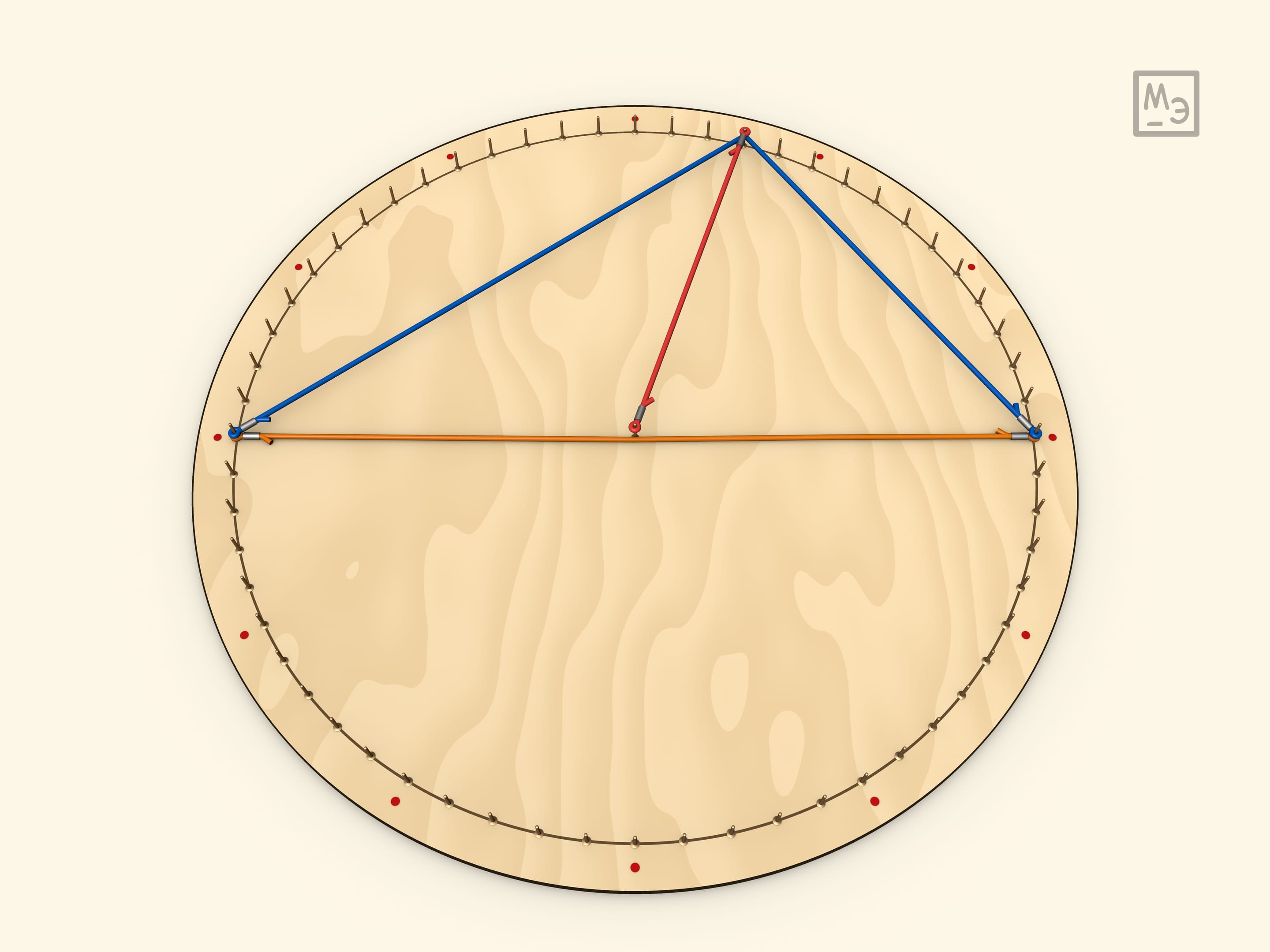
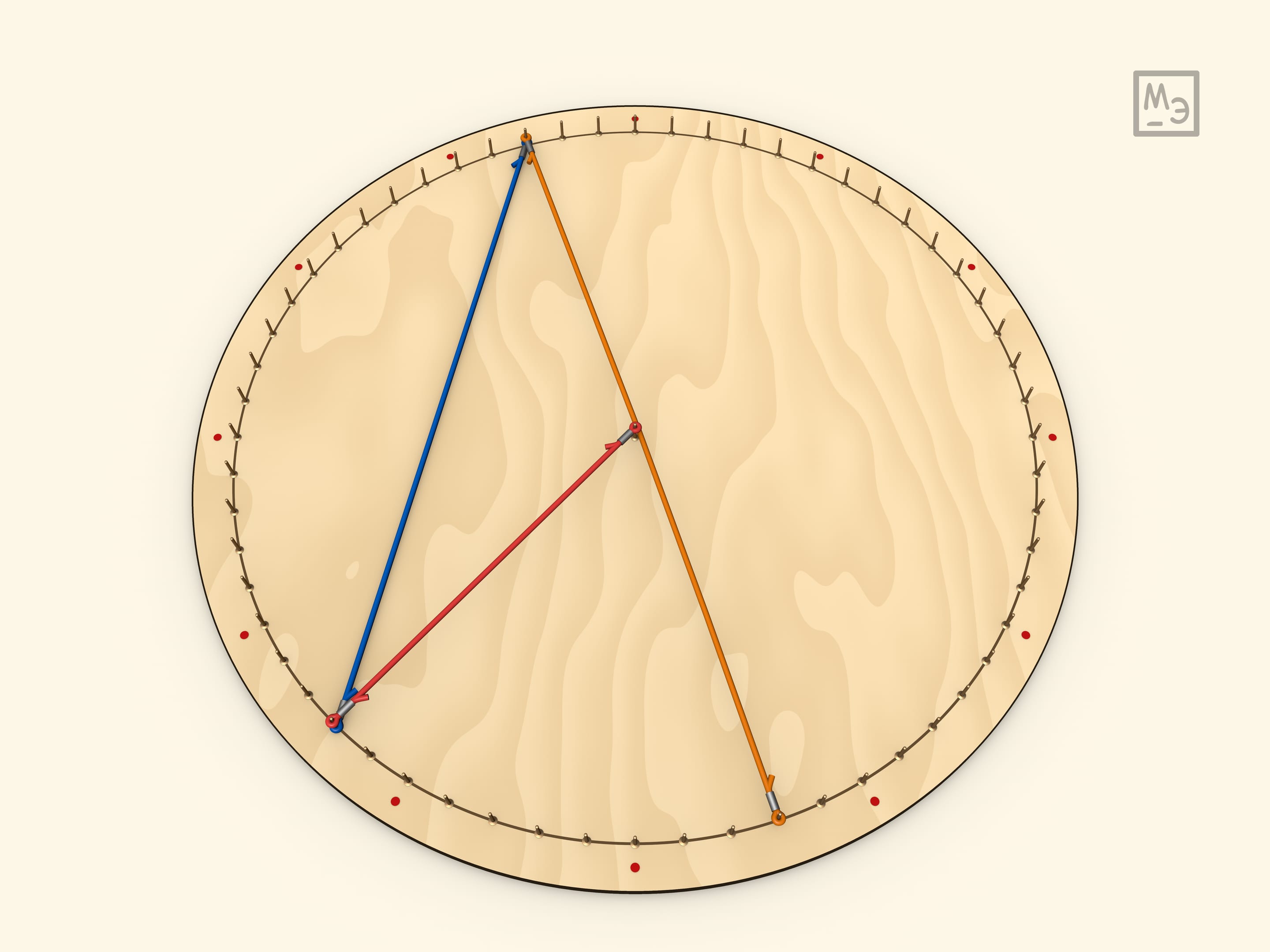
Первый шаг — рассмотреть вписанный угол, у которого одна из сторон является диаметром. Для доказательства вешается радиус. Полученный треугольник является равнобедренным, а значит, углы при его основании равны. А центральный угол для данного треугольника является внешним.
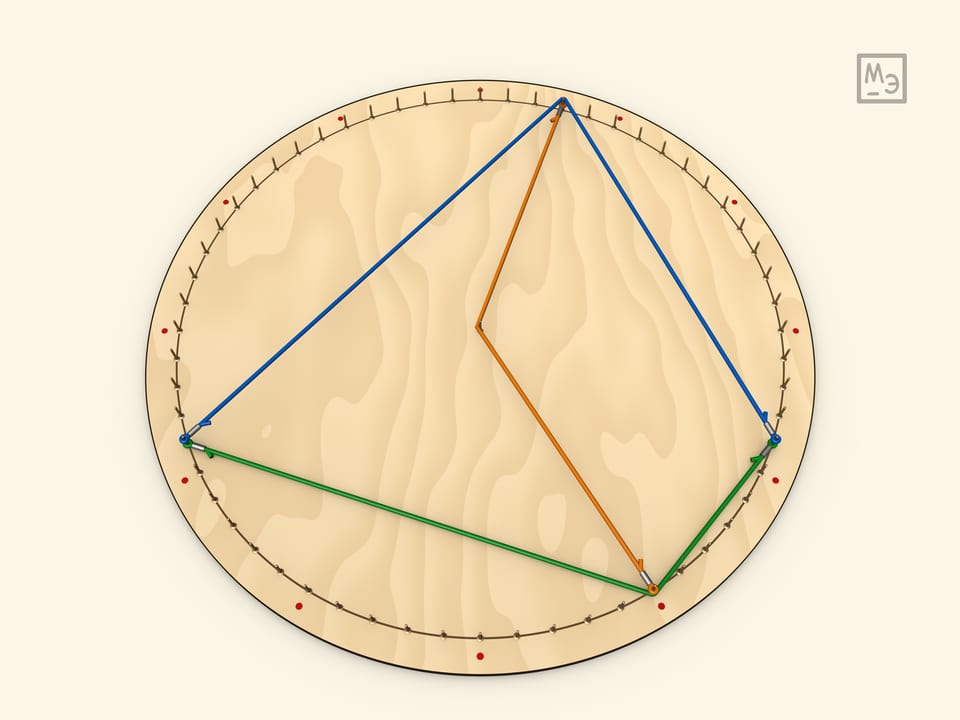
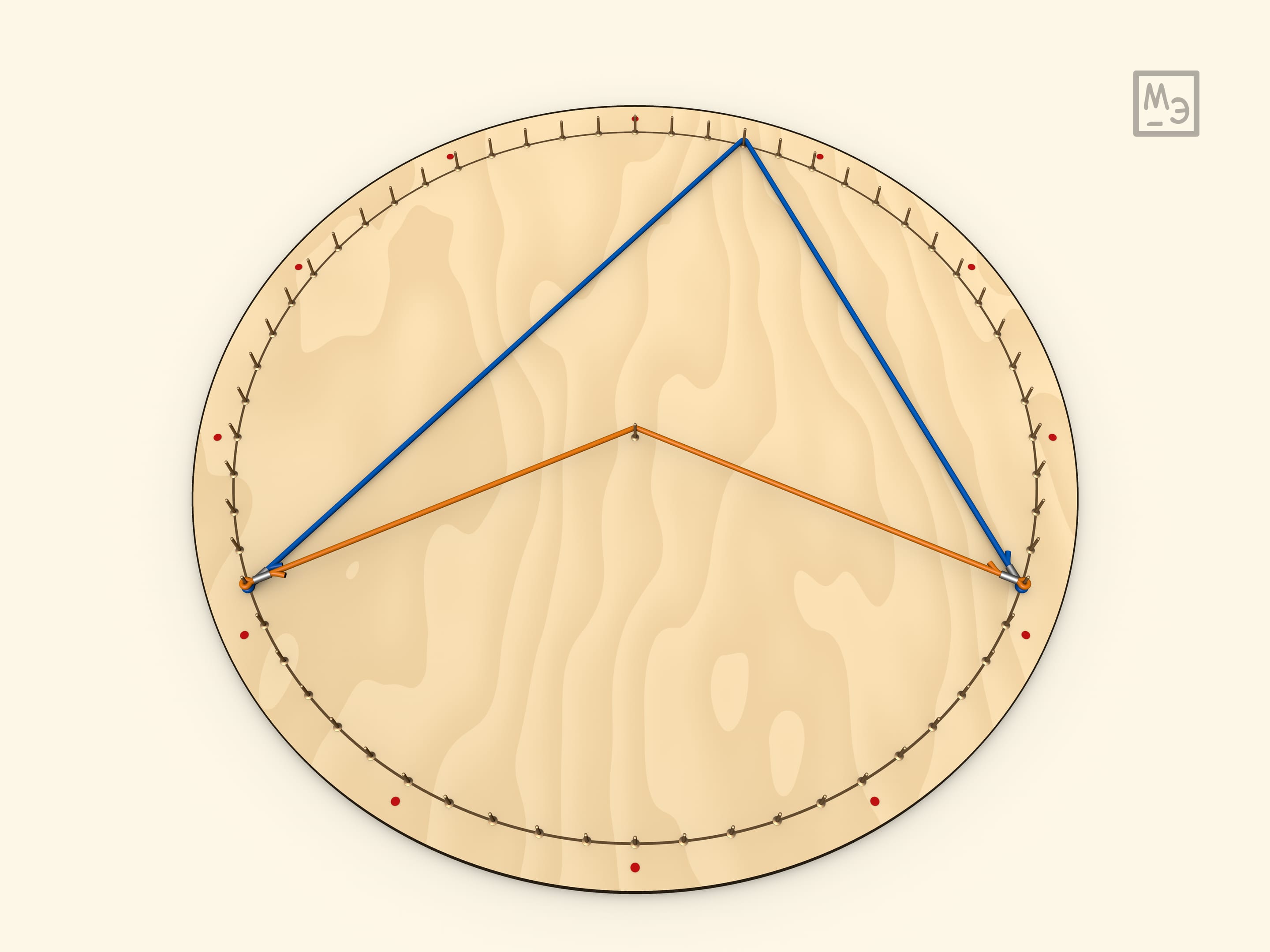
Любой вписанный угол равен половине центрального. Это доказывается проведением диаметра, что сводит задачу к предыдущему случаю.
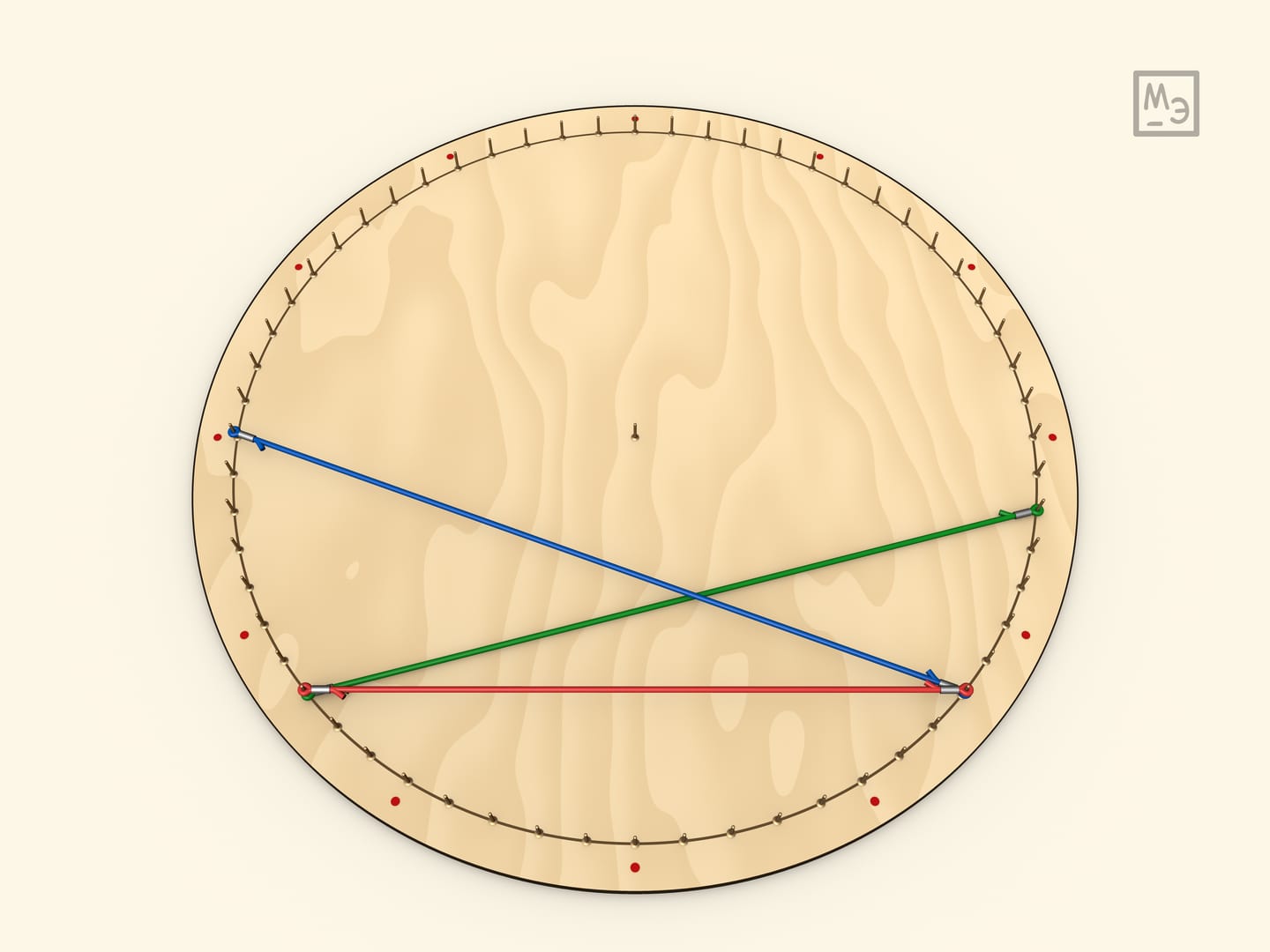
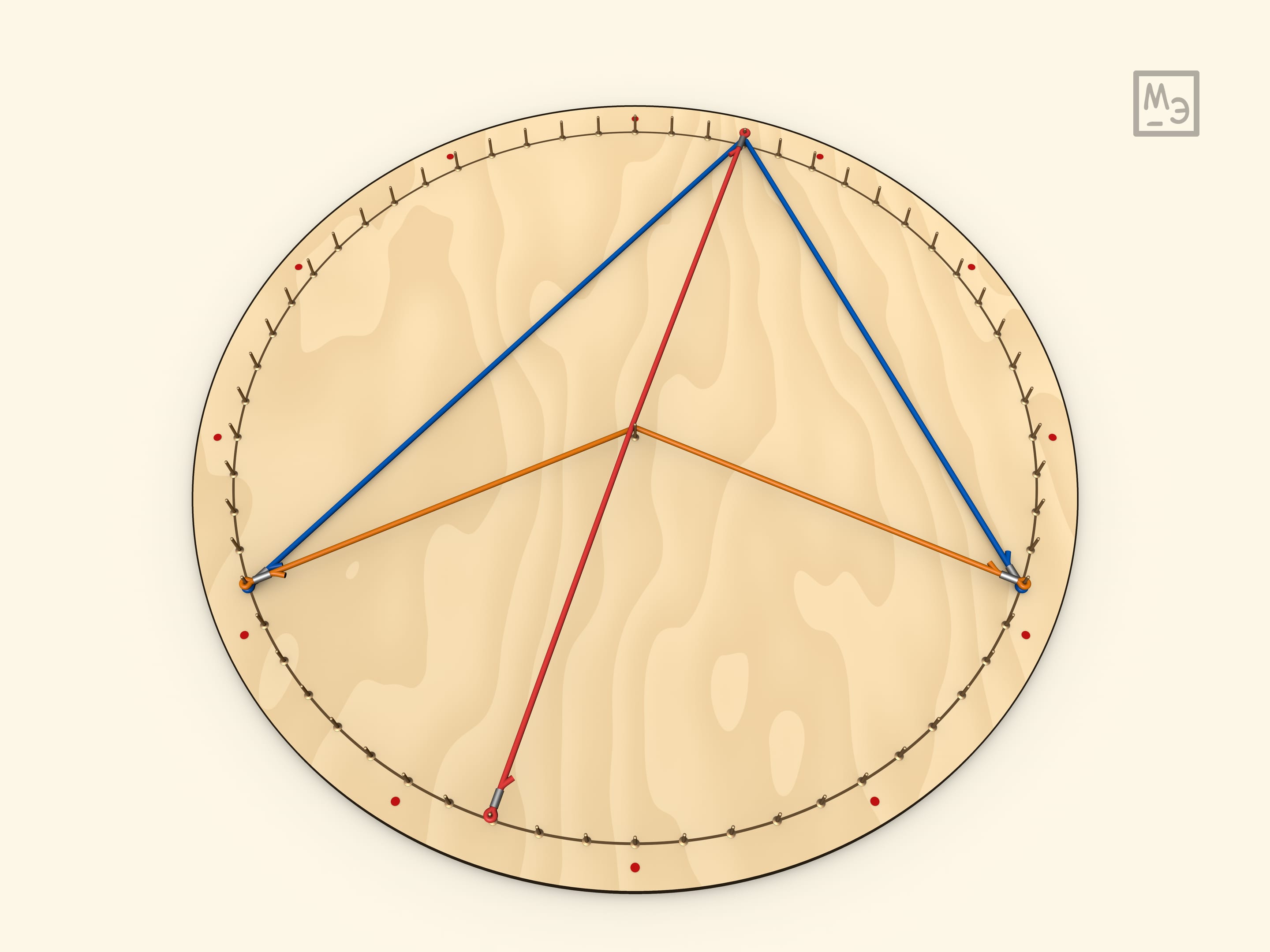
Последний случай, который часто смущает школьников, — когда диаметр не делит вписанный угол. Для доказательства следует рассматривать не сумму, а разность соответствующих углов.
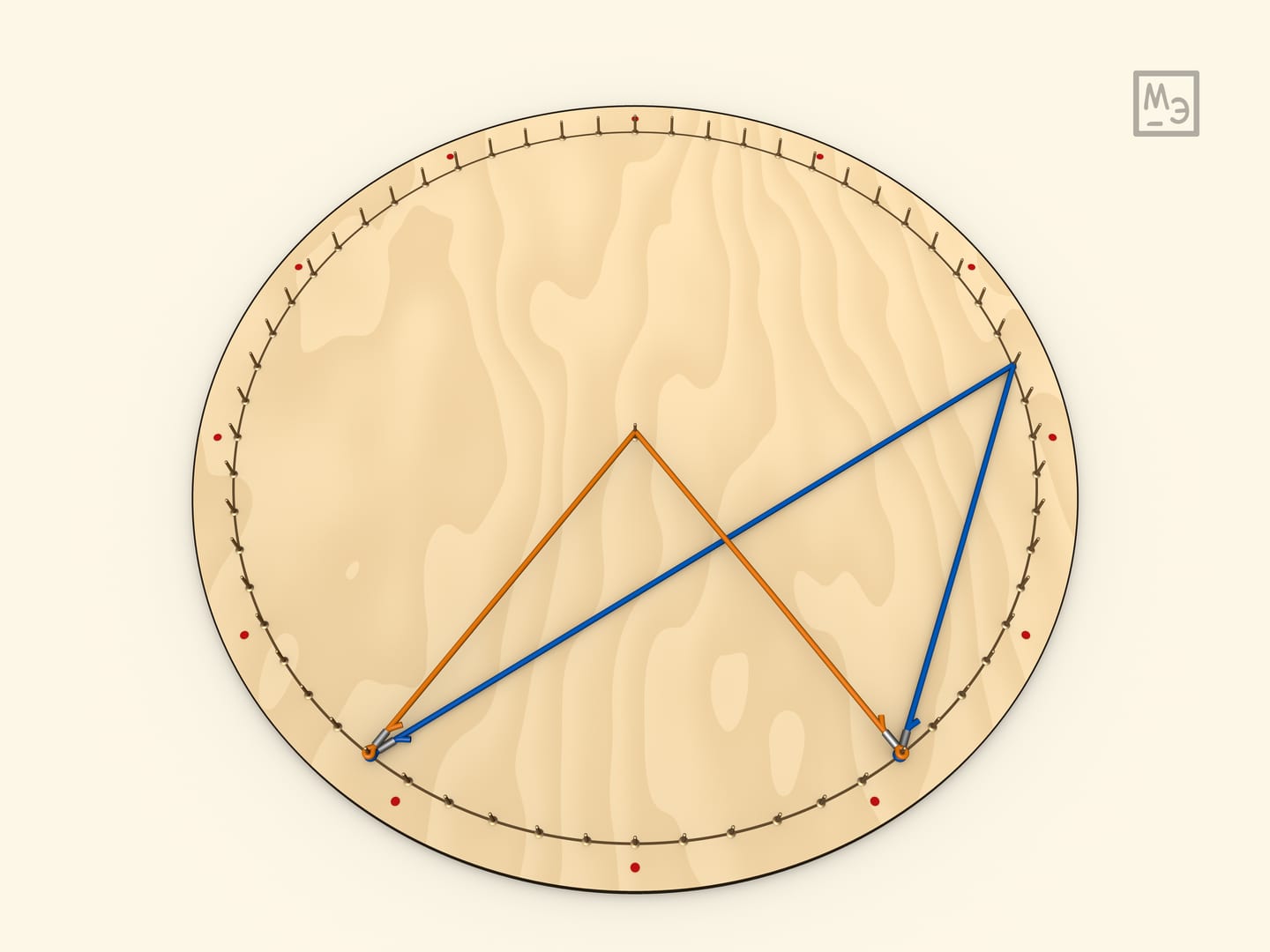
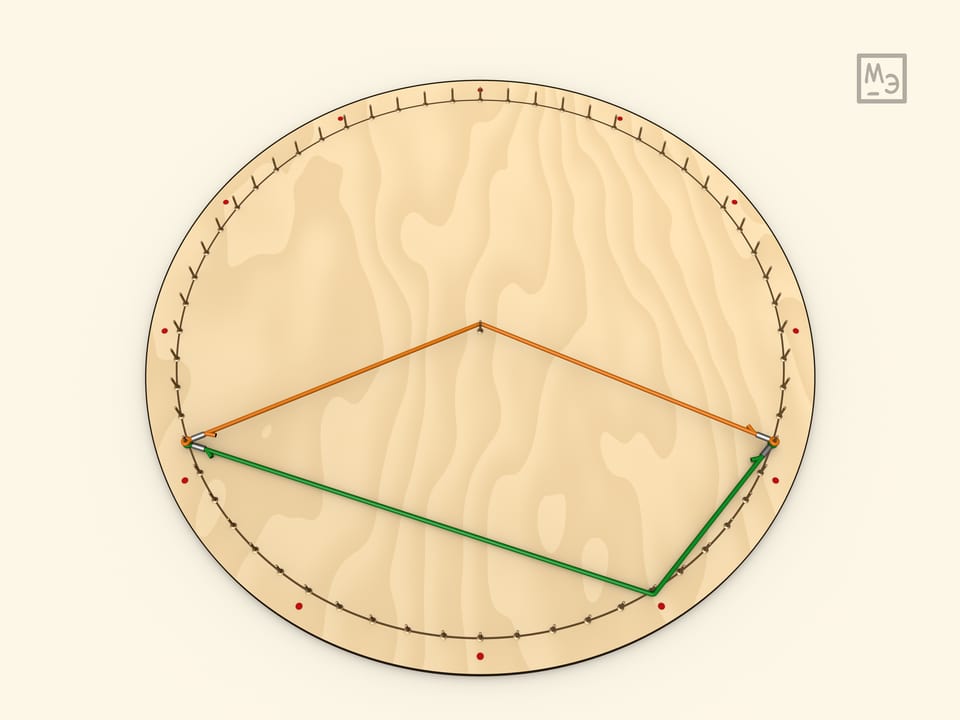
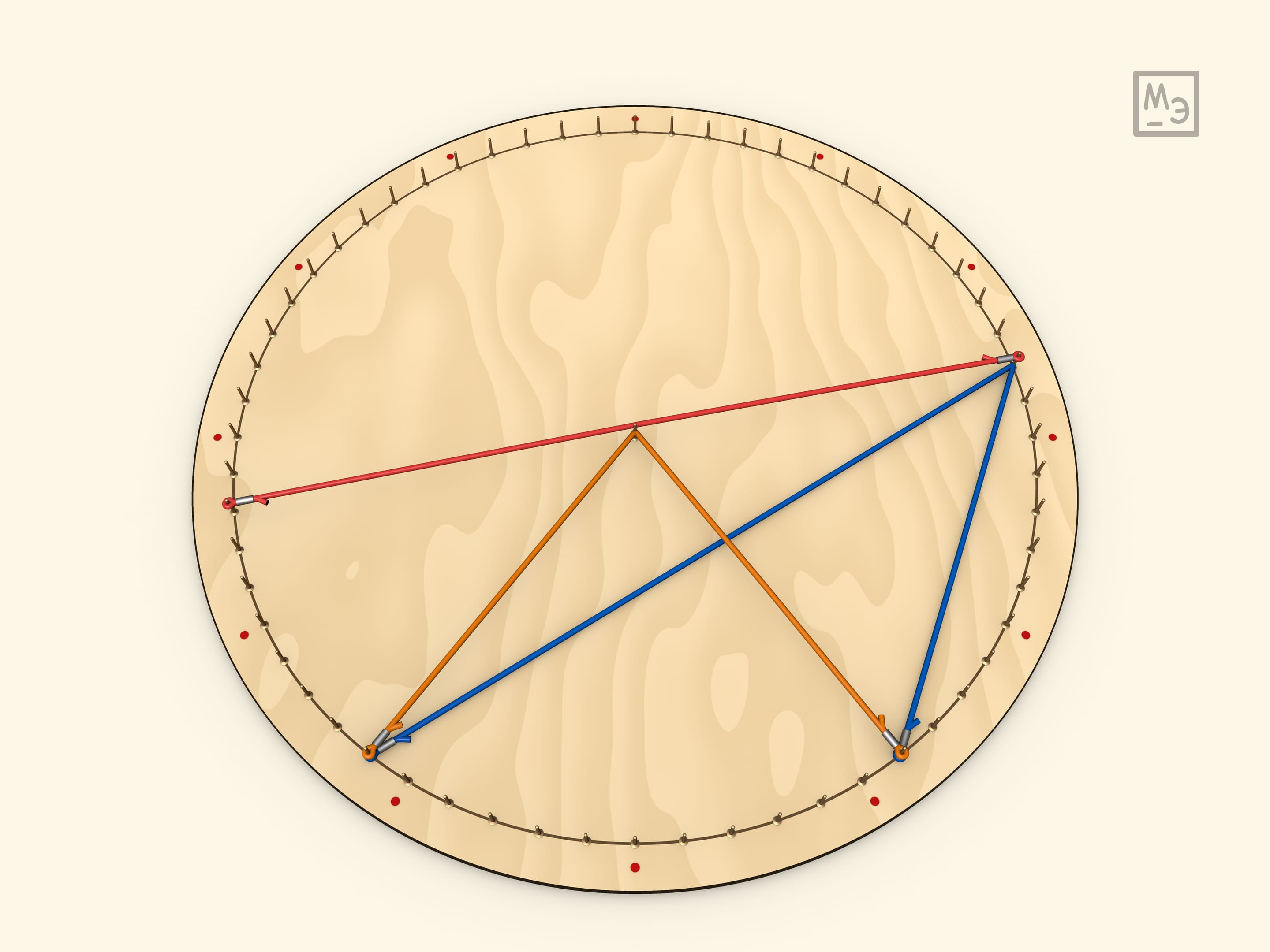
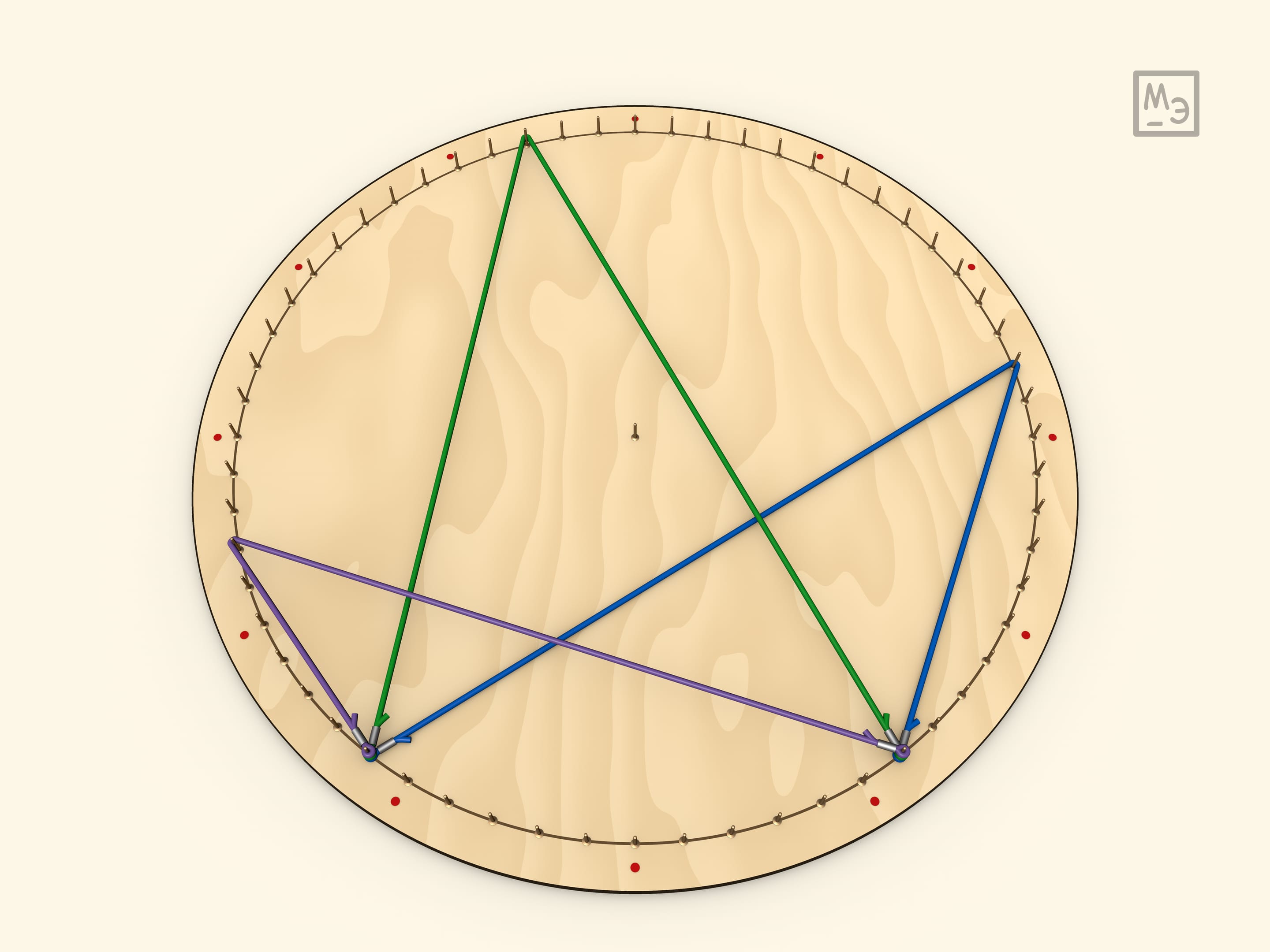
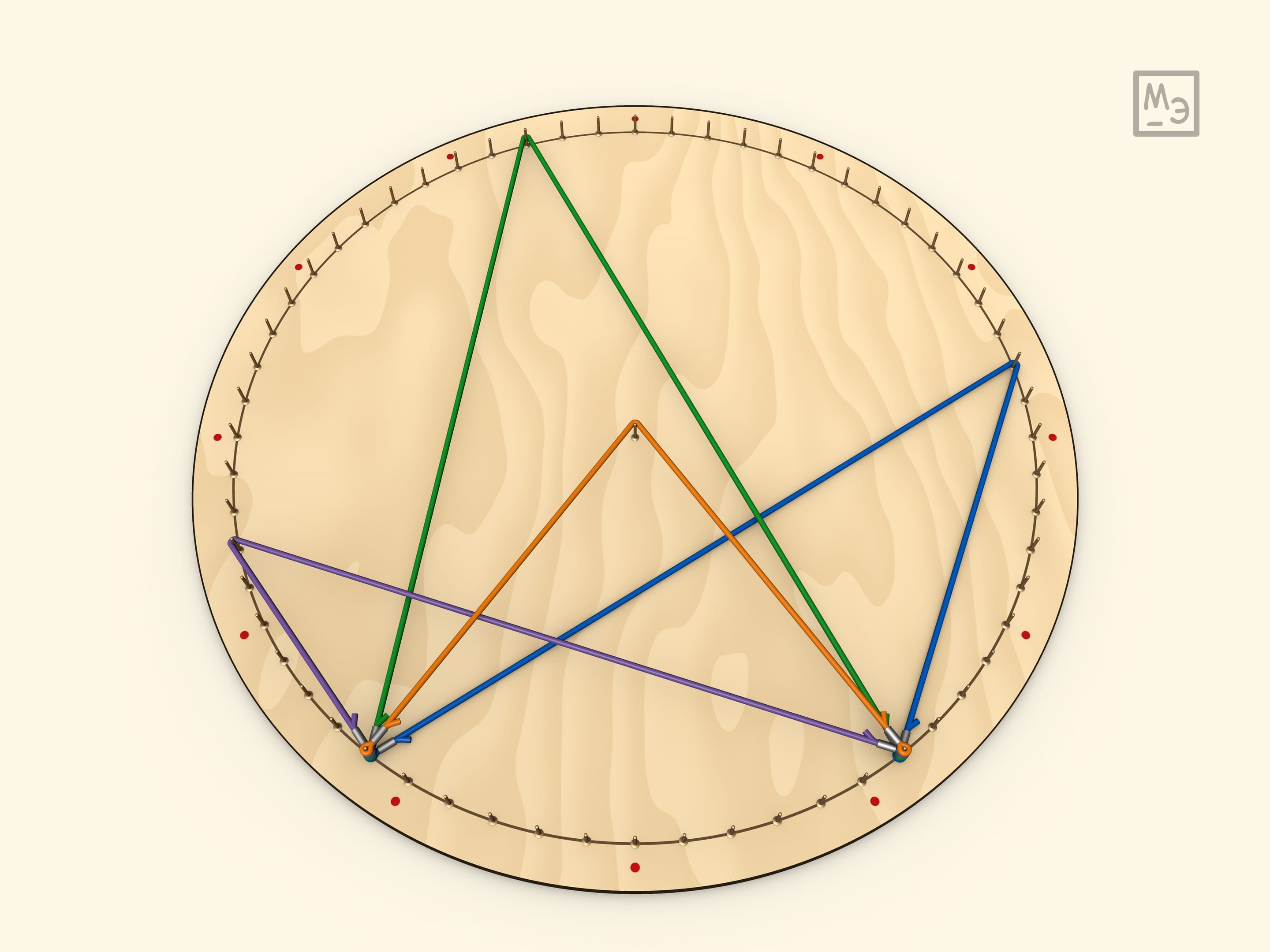
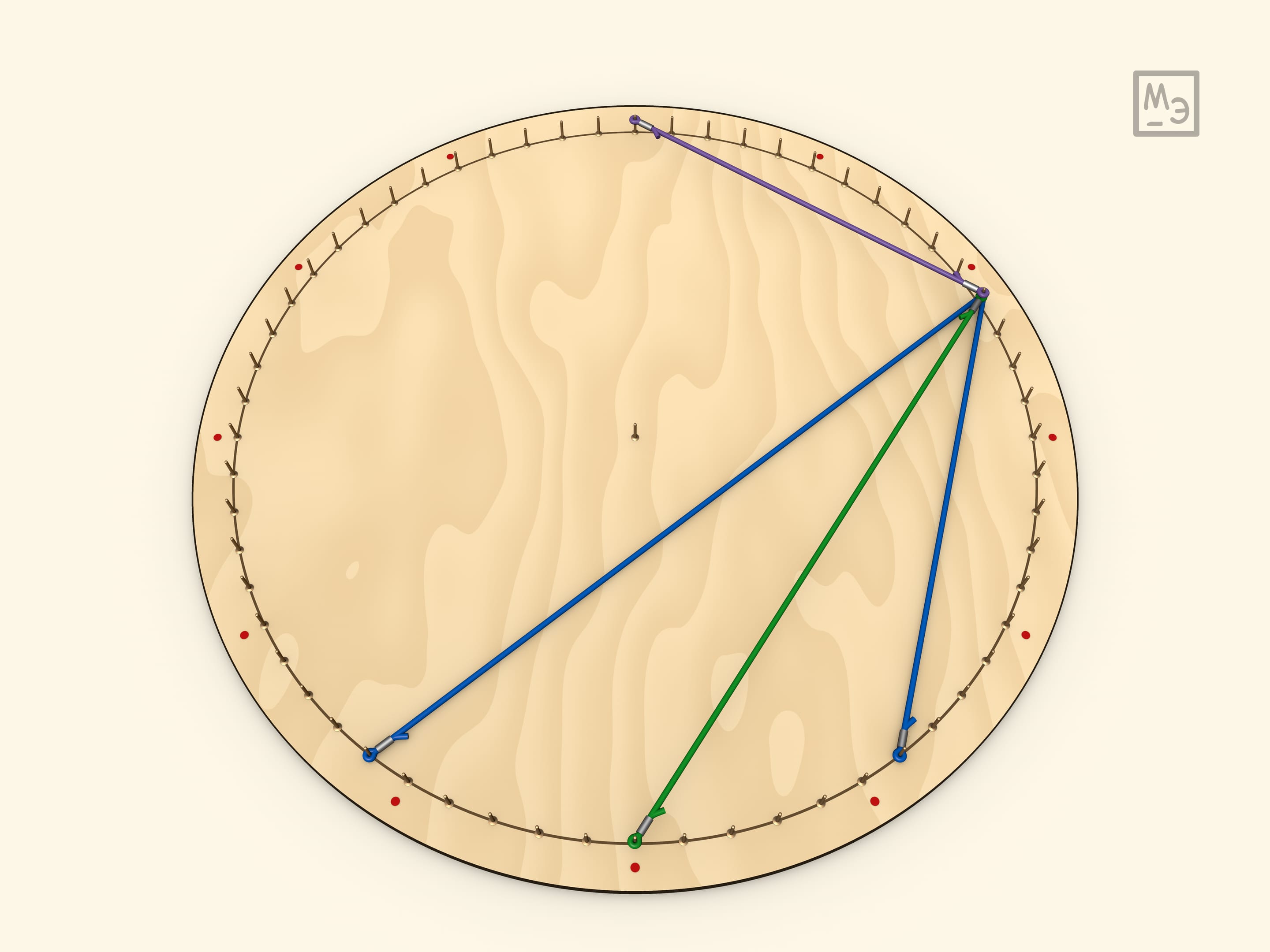
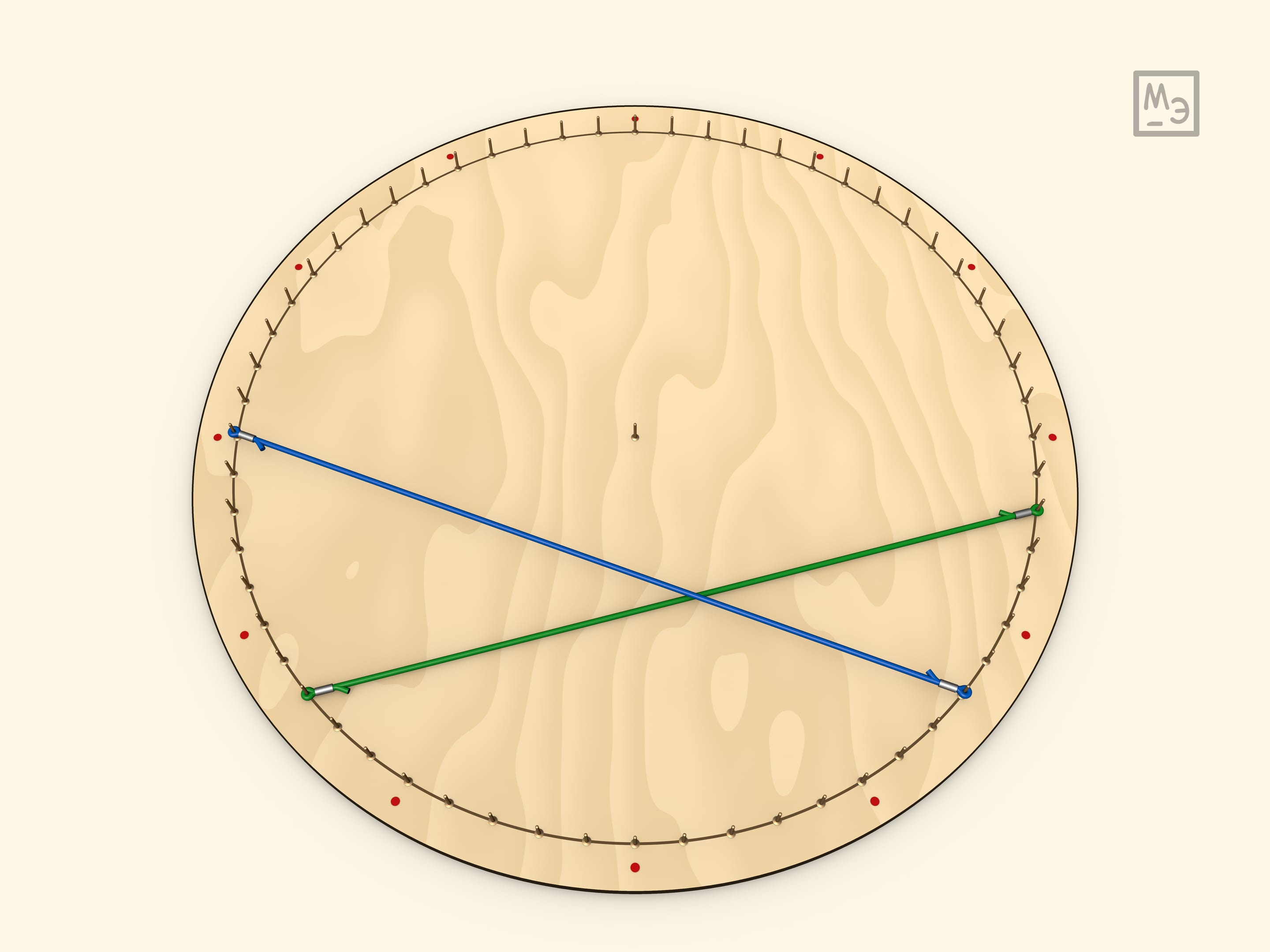
Итак, все углы, опирающиеся на одну дугу — равны (так как равны половине центрального угла).
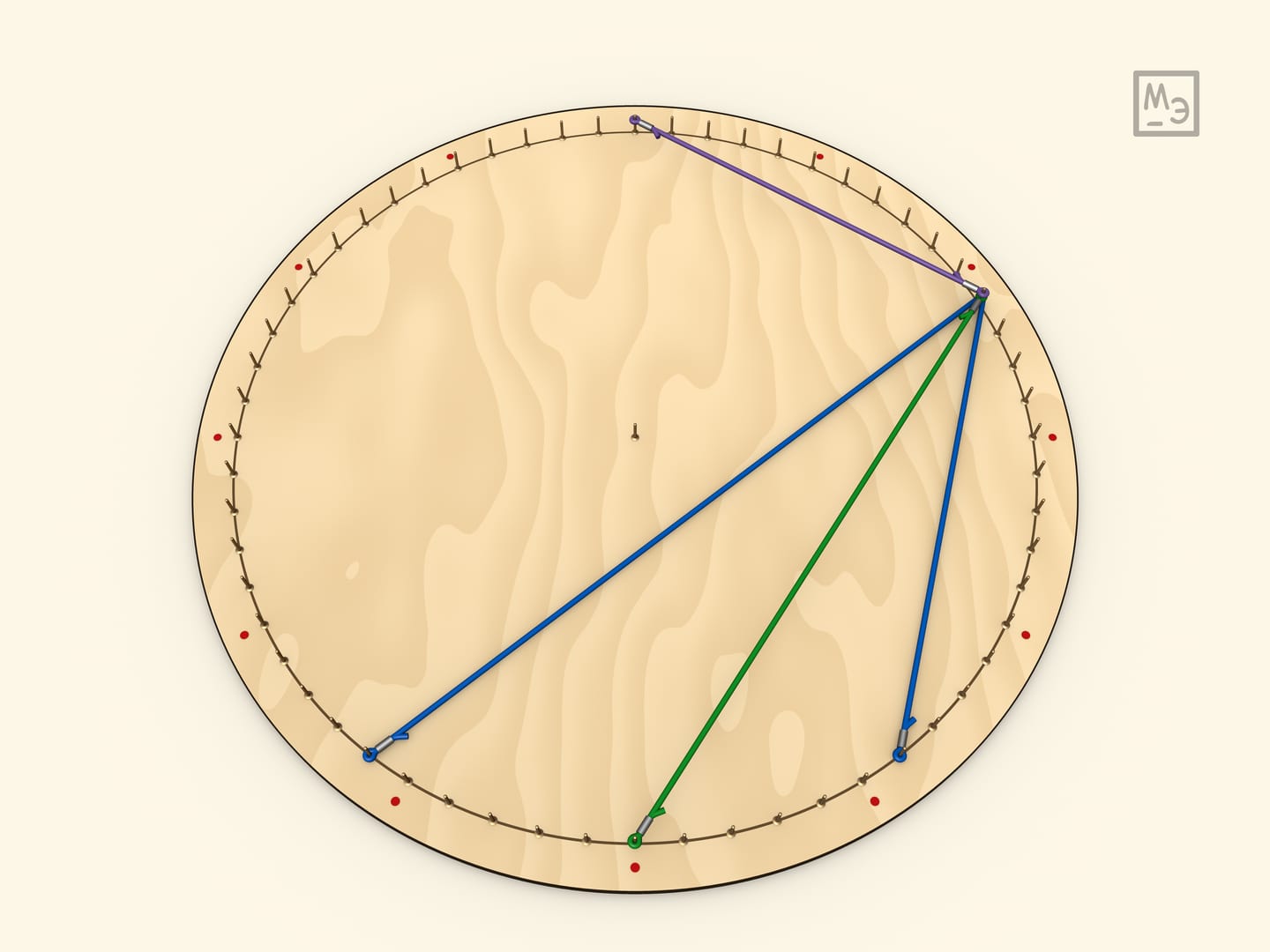
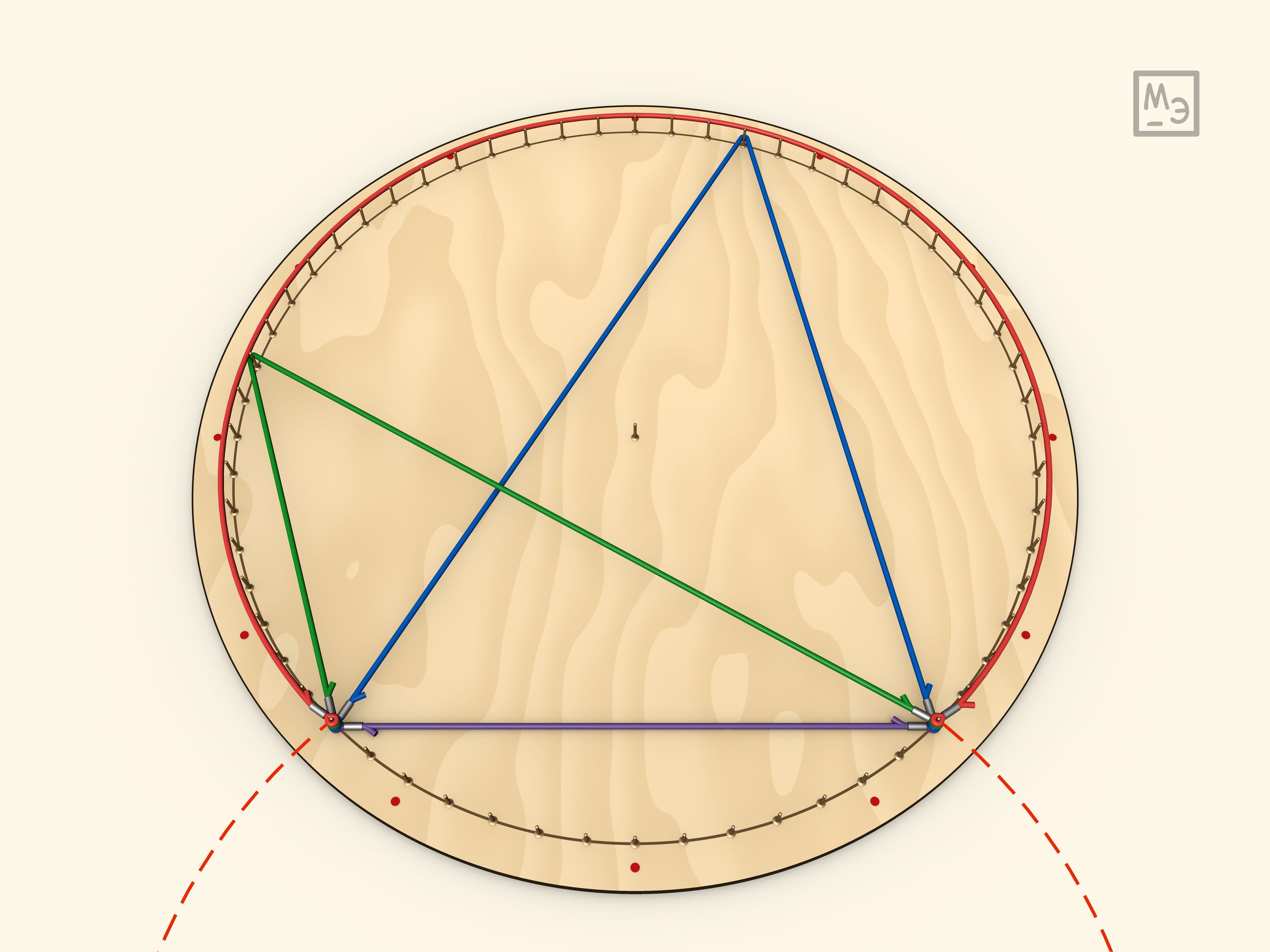
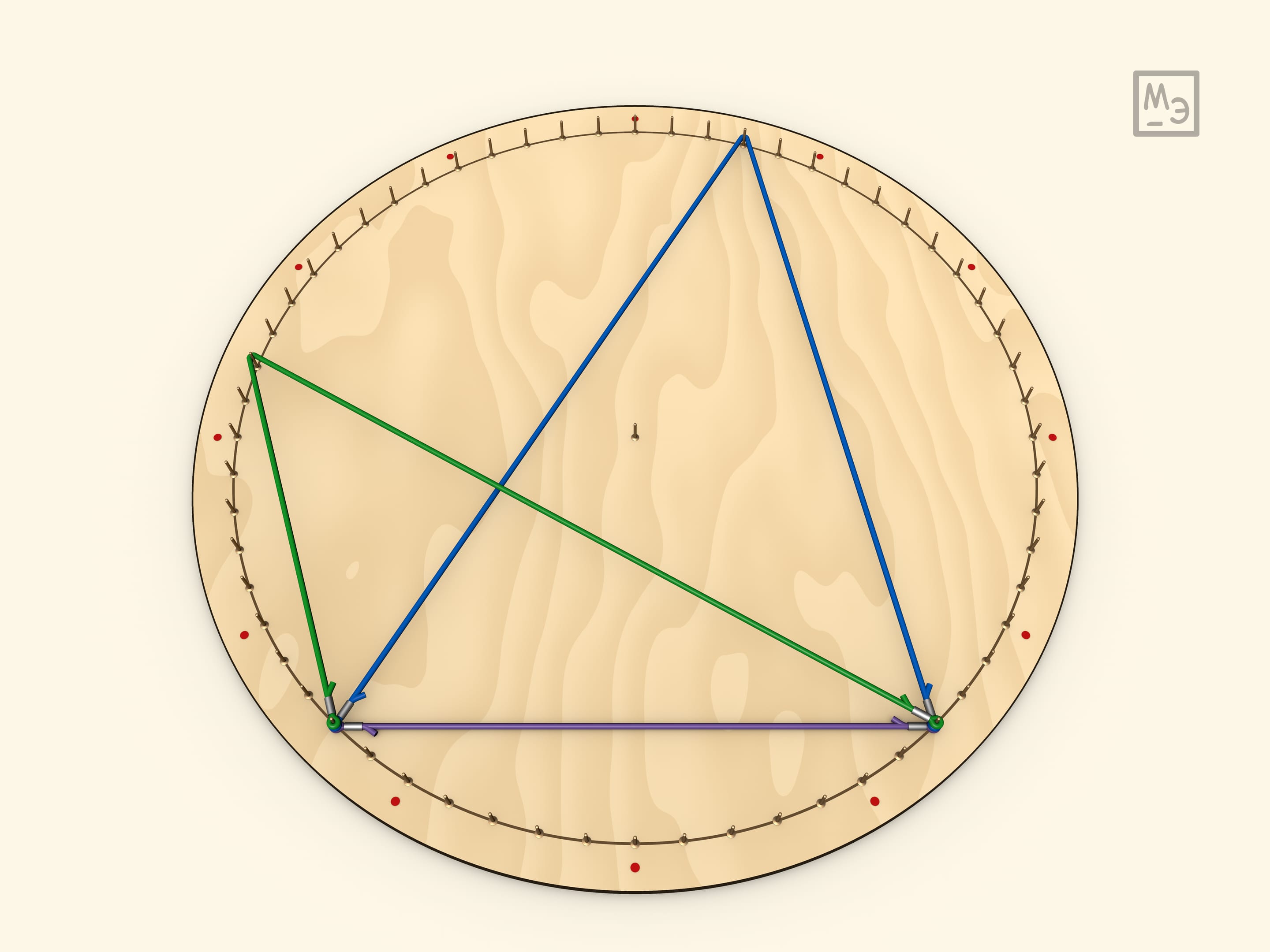
Чтобы построить биссектрису вписанного угла надо дугу поделить пополам (так же можно поделить угол на $3$, $4$, ... равные части). Интересно заметить, что биссектриса смежного угла приходит в диаметрально противоположную точку, так как биссектрисы смежных углов перпендикулярны. (Другой взгляд на этот же факт: середины дополнительных дуг — диаметрально противоположны.)
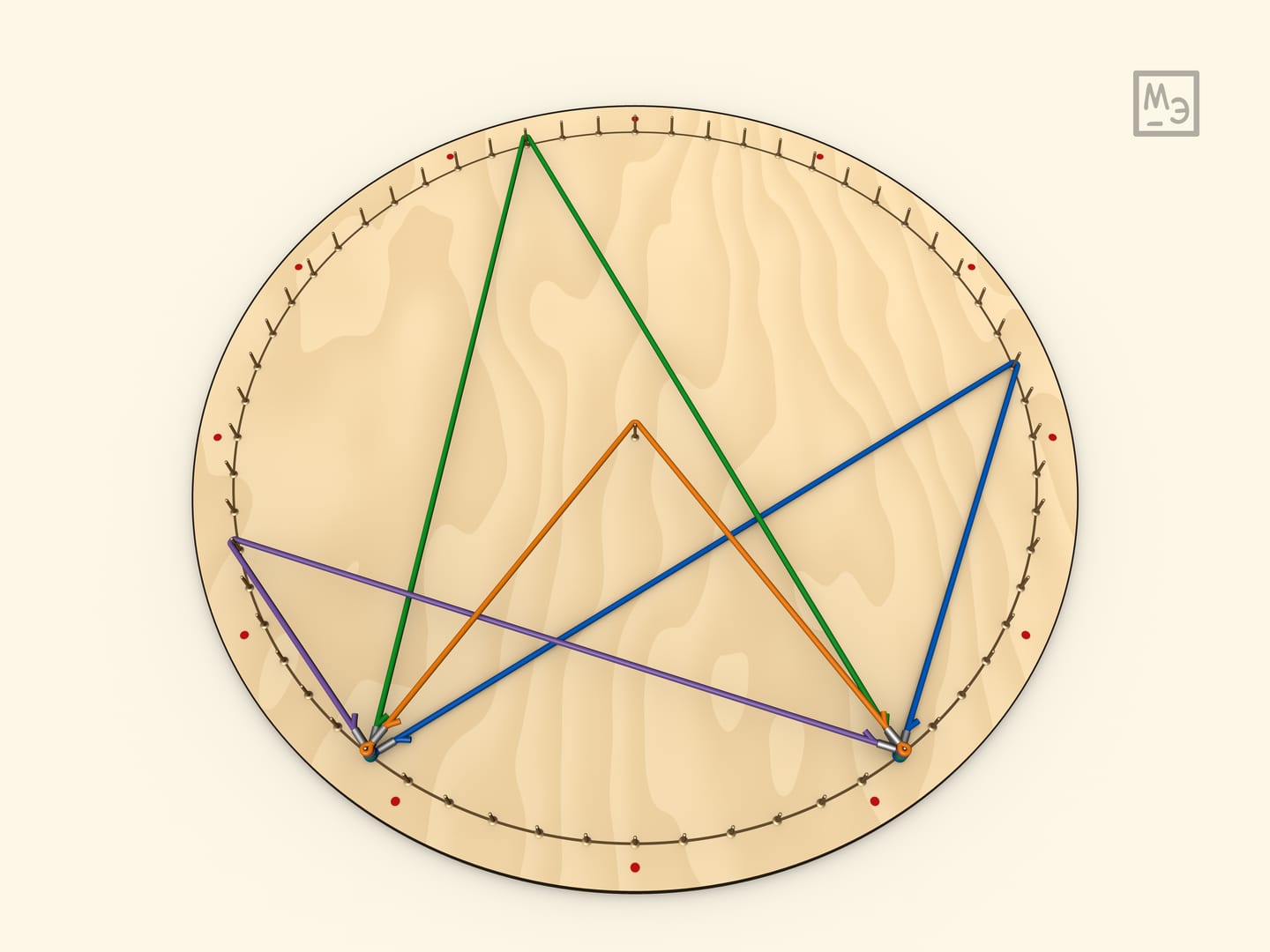
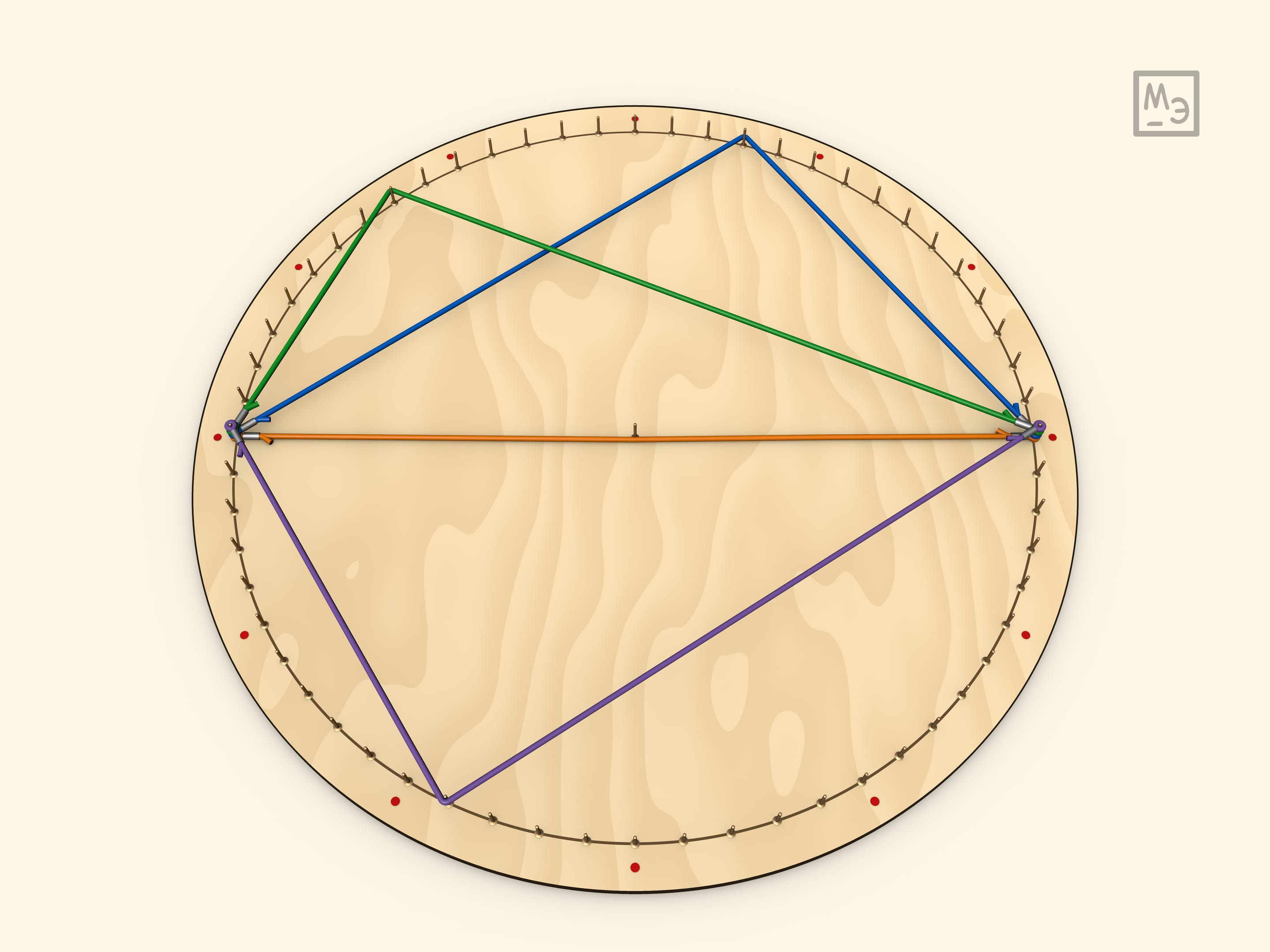
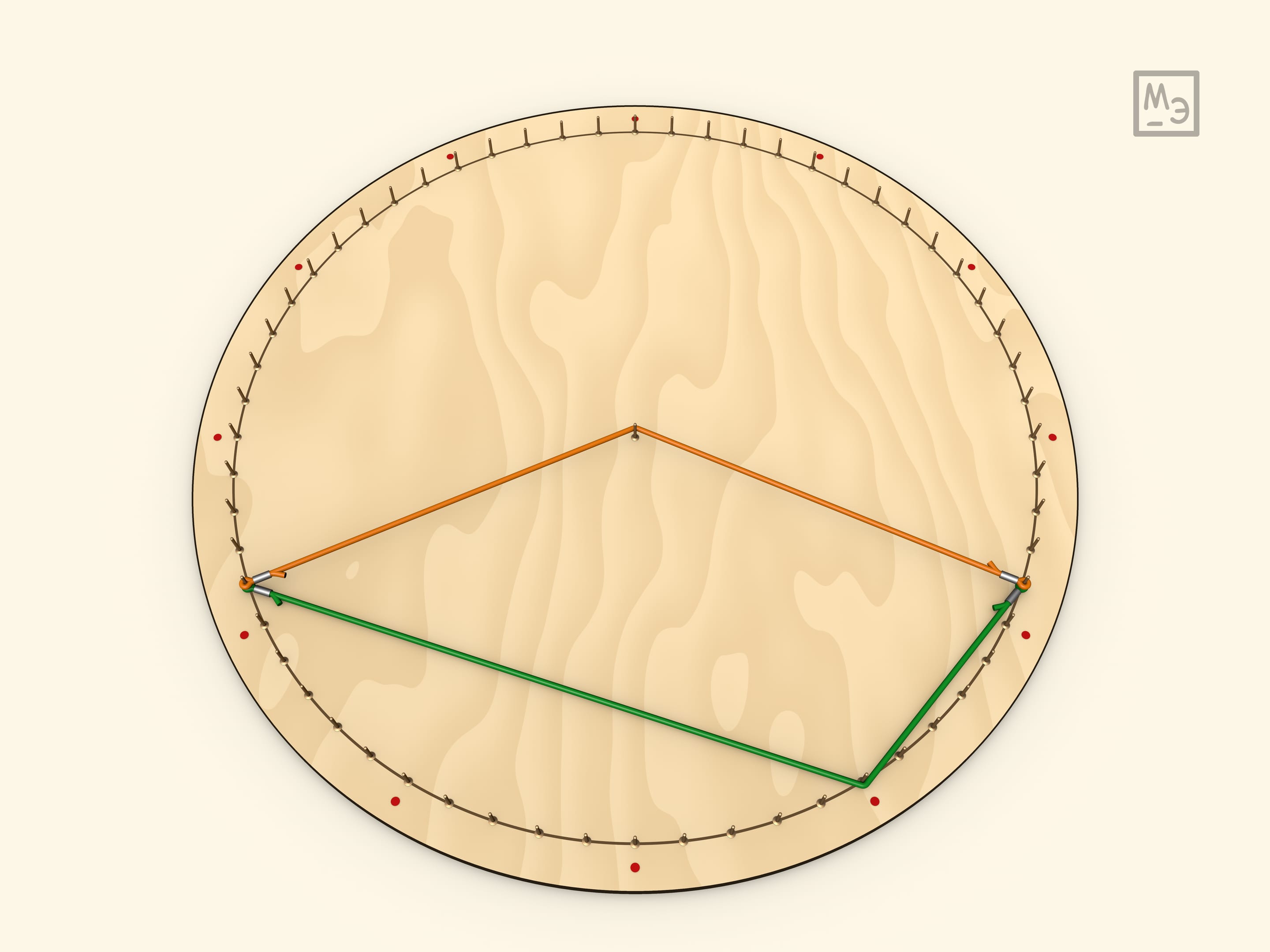
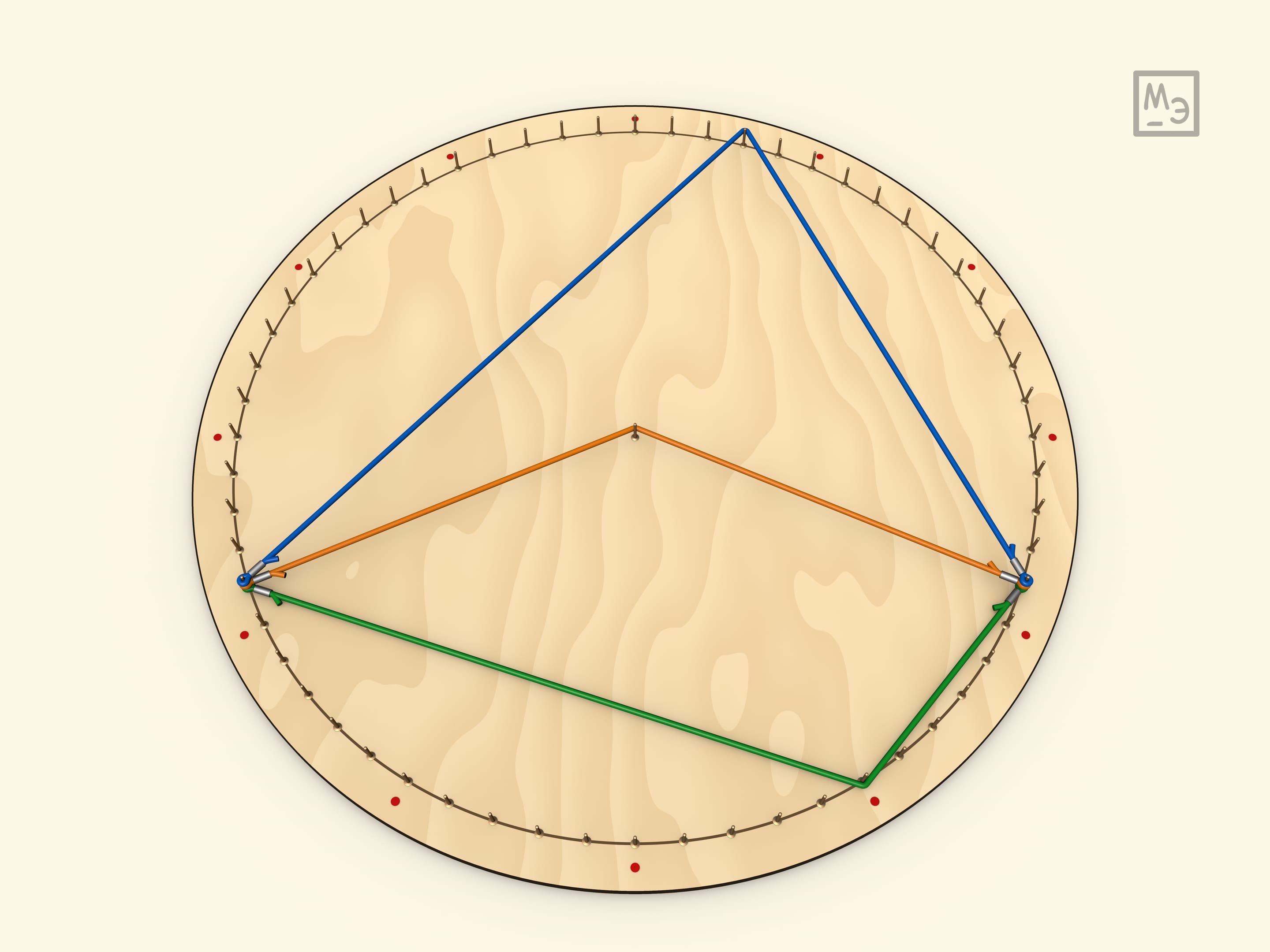
В случае, когда вписанный угол тупой, он всё так же равен половине соответствующего центрального (который в таком случае больше развёрнутого угла). Добавление резинки с теми же концами приводит к следующему утверждению: у вписанных в окружность четырёхугольников, сумма противоположных углов равна $180^\circ$. Перевешивание центрального угла показывает, что это не зависит от того какую пару противоположных углов рассматривать.
К теме вписанных углов примыкает задача определить геометрическое место точек, из которых данный отрезок виден под данным углом. Решение которой — в фольклоре «уши чебурашки» — две дуги окружностей, построенных на этом отрезке.
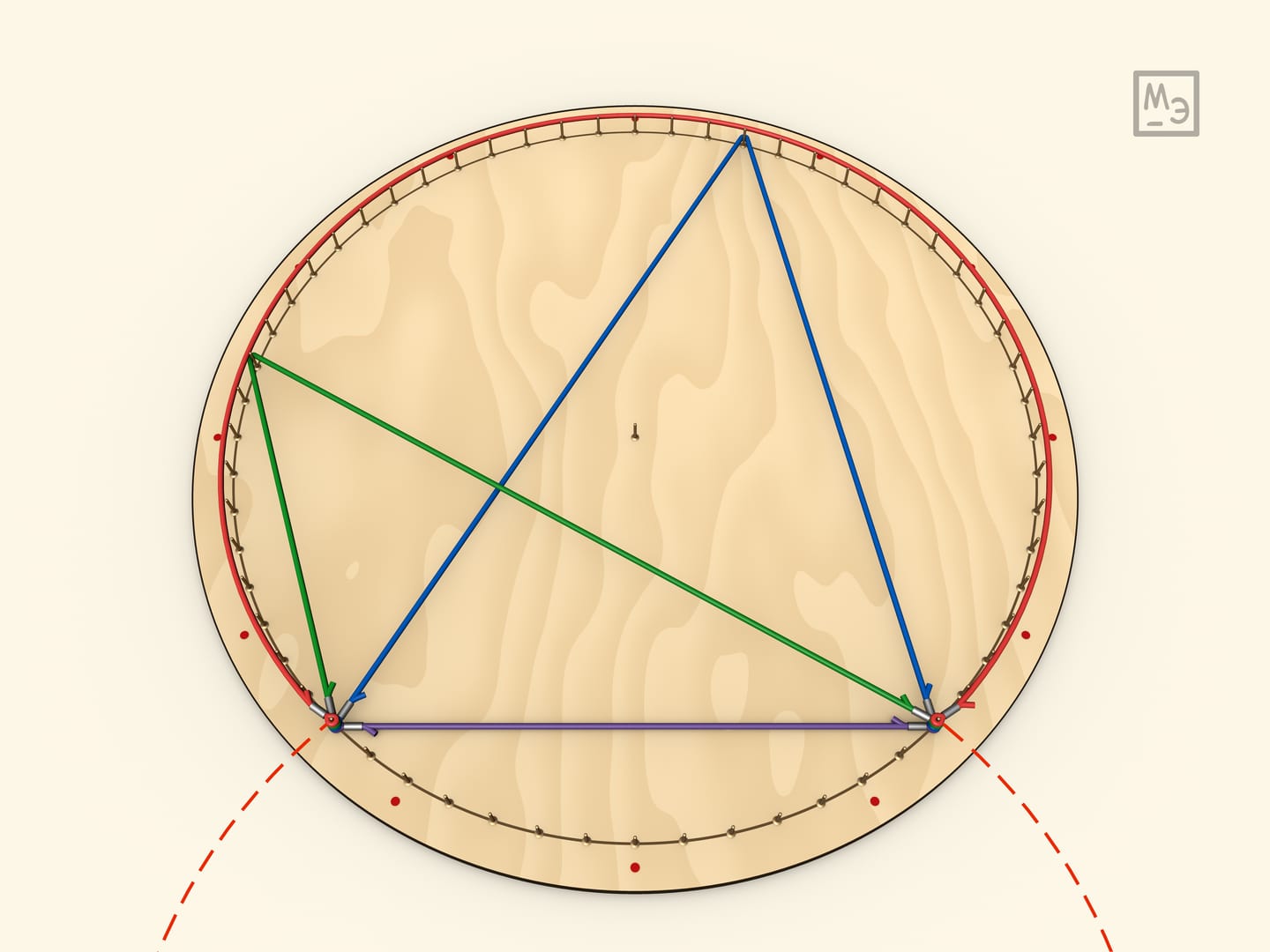
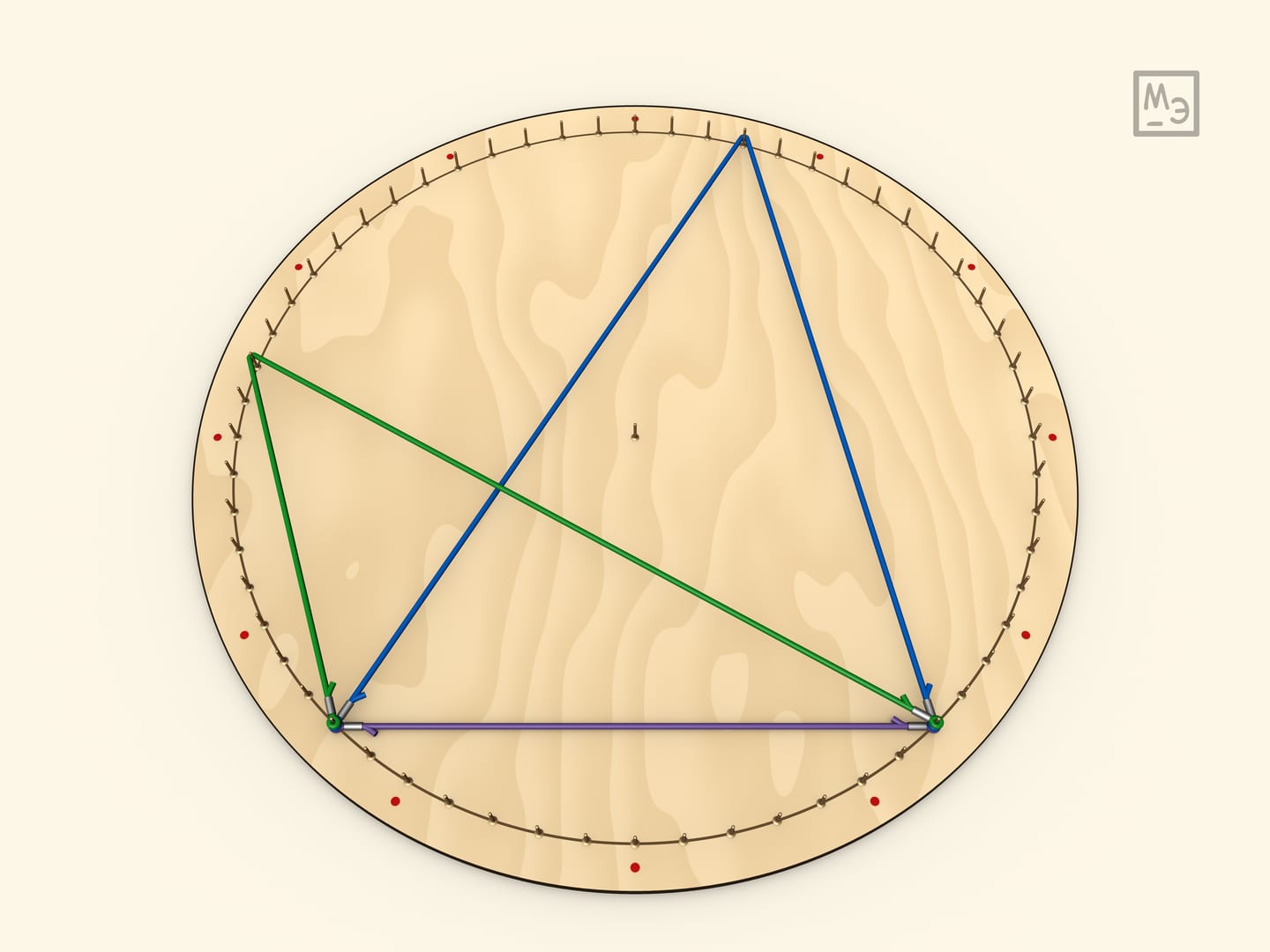
Из того, что вписанные углы, опирающиеся на одну дугу равны выводится интересный факт: радиус описанной около треугольника окружности определяется стороной и противолежащим углом. (Хотя обычно, элементы треугольника зависят от трёх его характеристик!). Отсюда выводится теорема синусов $\frac{a}{\sin\alpha}=2r$.
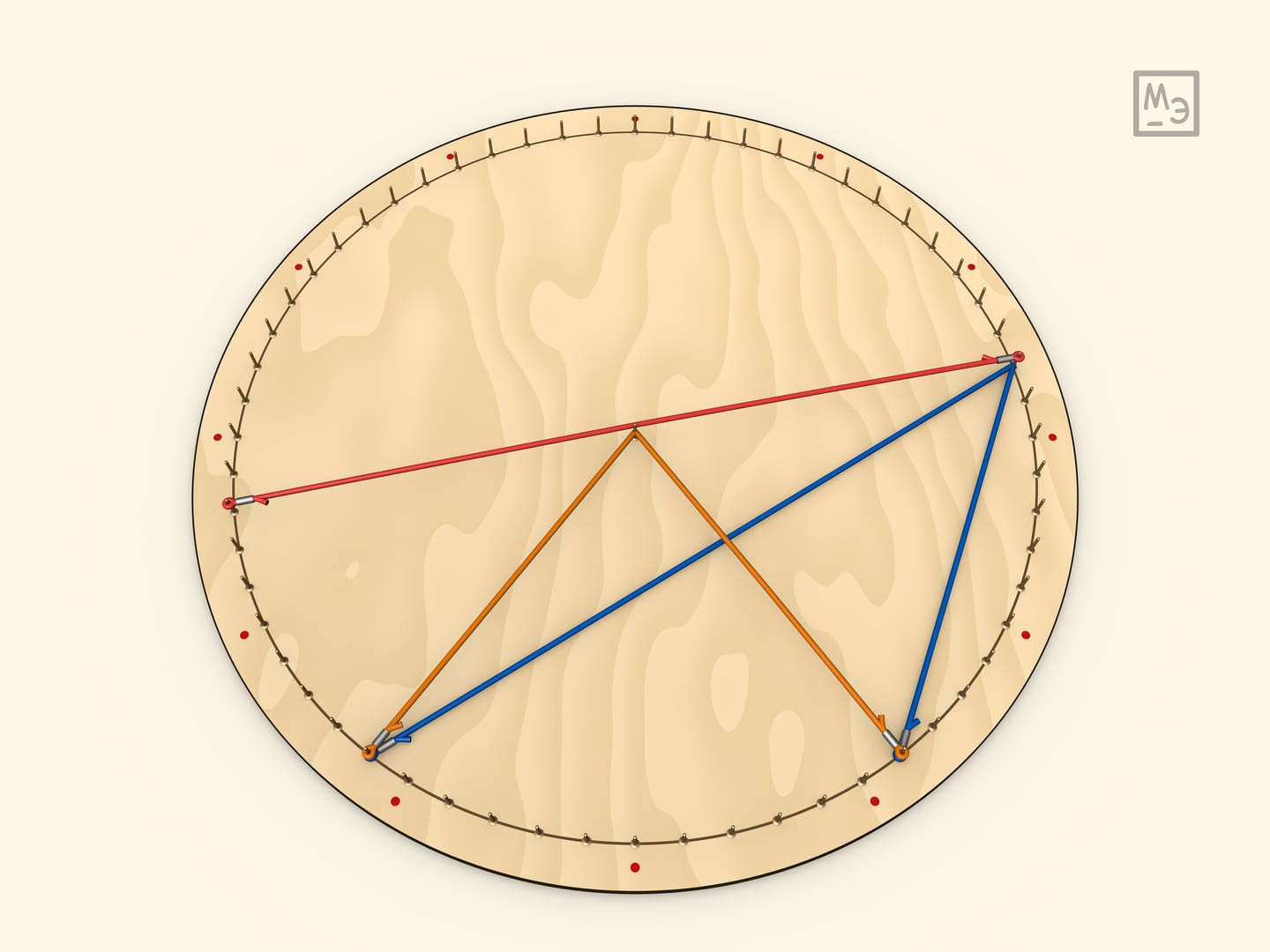
Из утверждения, что вписанный угол равен половине центрального, выводится следующее утверждение: угол между хордами равен полусумме дуг. Для доказательства вешается дополнительная резинка. Например, так считаются углы между диагоналями правильного $n$-угольника. (Если хорды не пересекаются, то аналогично показывается, что угол равен полуразности дуг).
Если диаметр круга сделать в ширину листа А4, то будет легко дополнить модель сменными листочками, одевающимися на центральный столбик. Это можно использовать для нанесения дополнительных построений. Если круг сделать из пластика, то для дополнительных построений можно просто использовать маркер. Можно из разноцветной бумаги вырезать кружочки и вкладывать их для наглядности в углы которые исследуются.