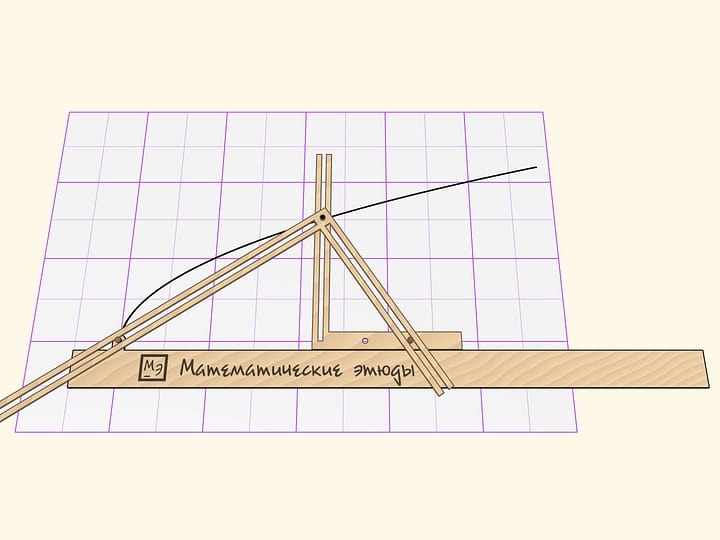
Оптическое свойство параболы является основой впечатляющей игрушки: на крышке «летающей тарелки» вы видите объект, осязаемо‐объёмный, пытаетесь его взять, и… пальцы встречают пустоту.
Игрушка состоит из двух соосных параболоидов вращения, чаши которых обращены друг к другу, «шапочка» верхней чаши срезана. На нижней чаше, в фокусе верхнего параболоида находится объект; после отражений в зеркальных стенках параболоидов в фокусе нижнего формируется изображение.
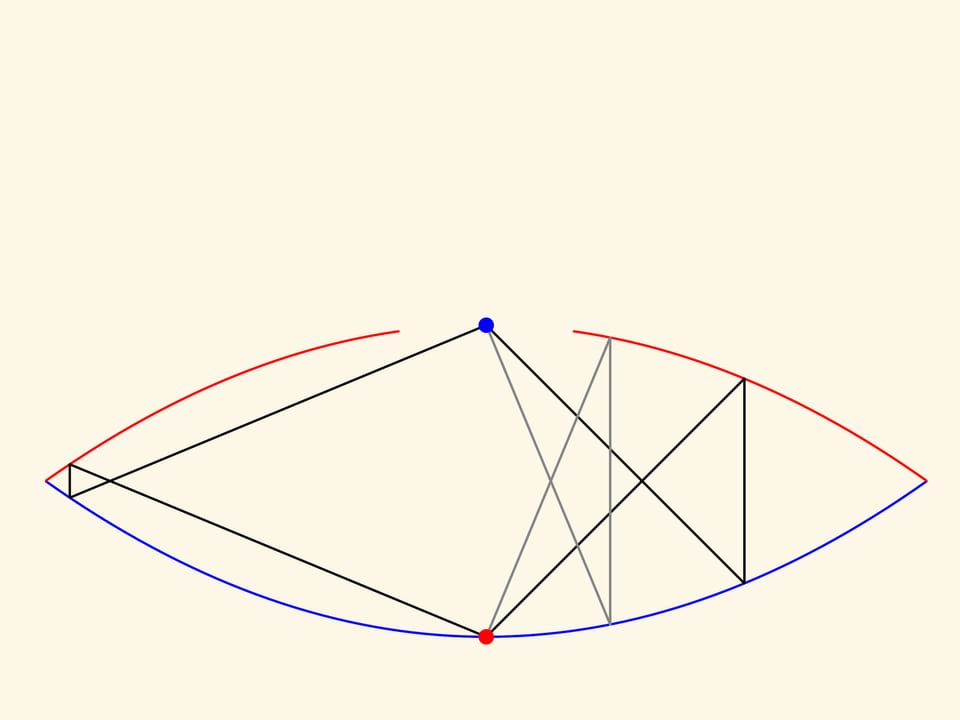
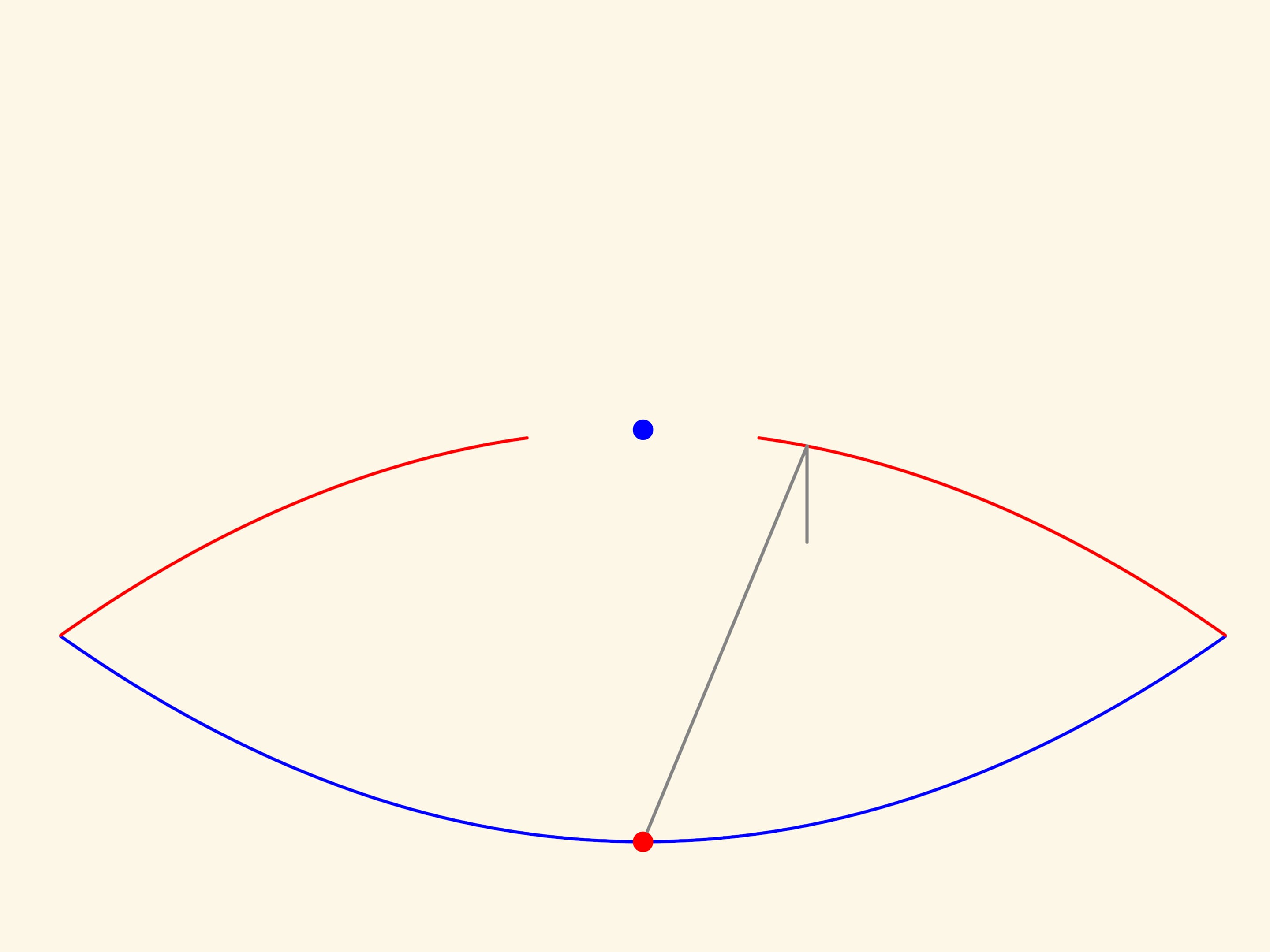
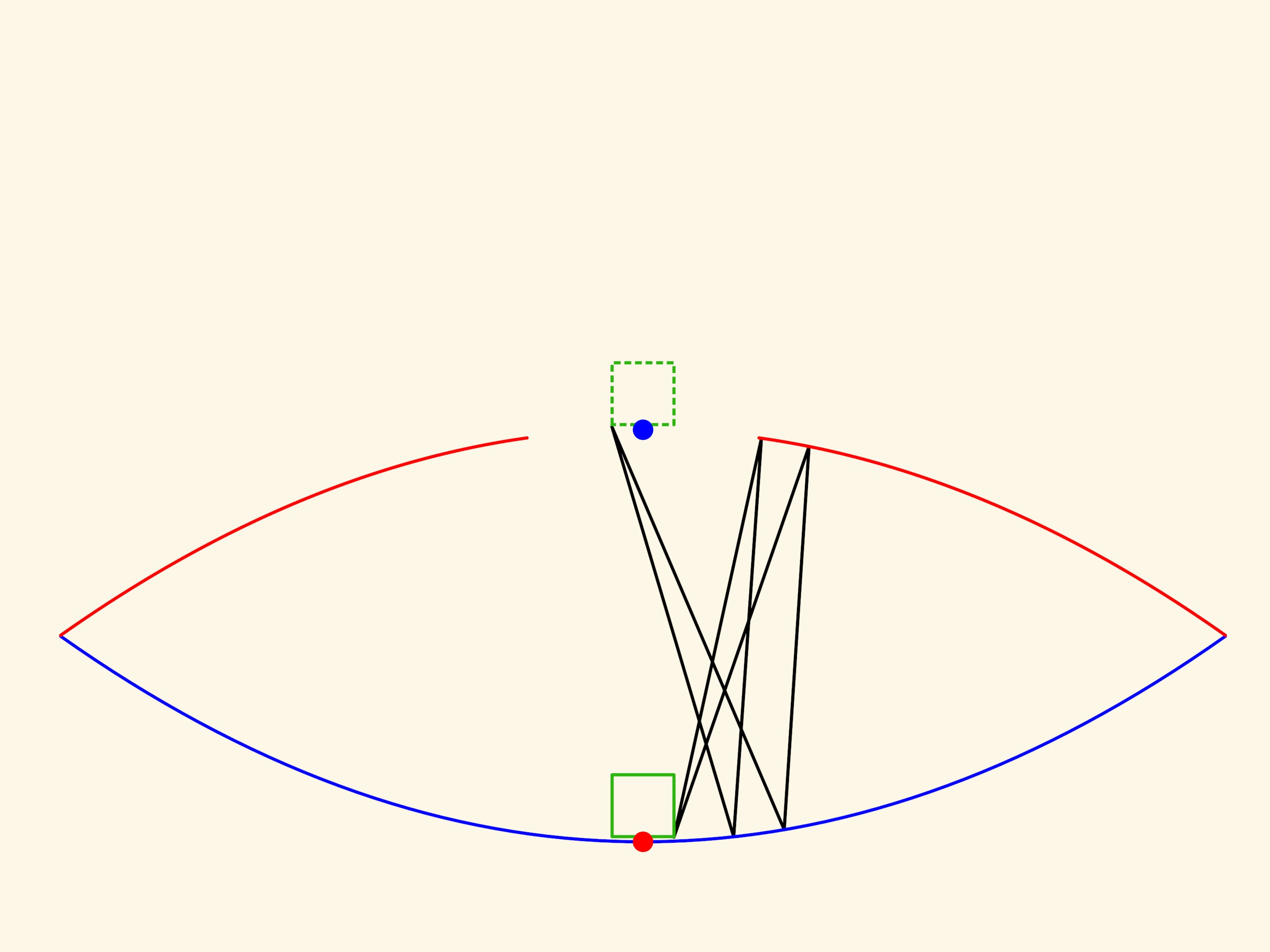
Рассмотрим плоское сечение модели. Согласно оптическому свойству параболы, если луч вышел из фокуса красной параболы, то после отражения от неё луч пойдёт параллельно оси. И поскольку параболы соосны, то к синей параболе он придёт параллельно оси, а значит, после отражения попадёт в её фокус. И так будет с любым лучом, вышедшим из фокуса красной параболы.
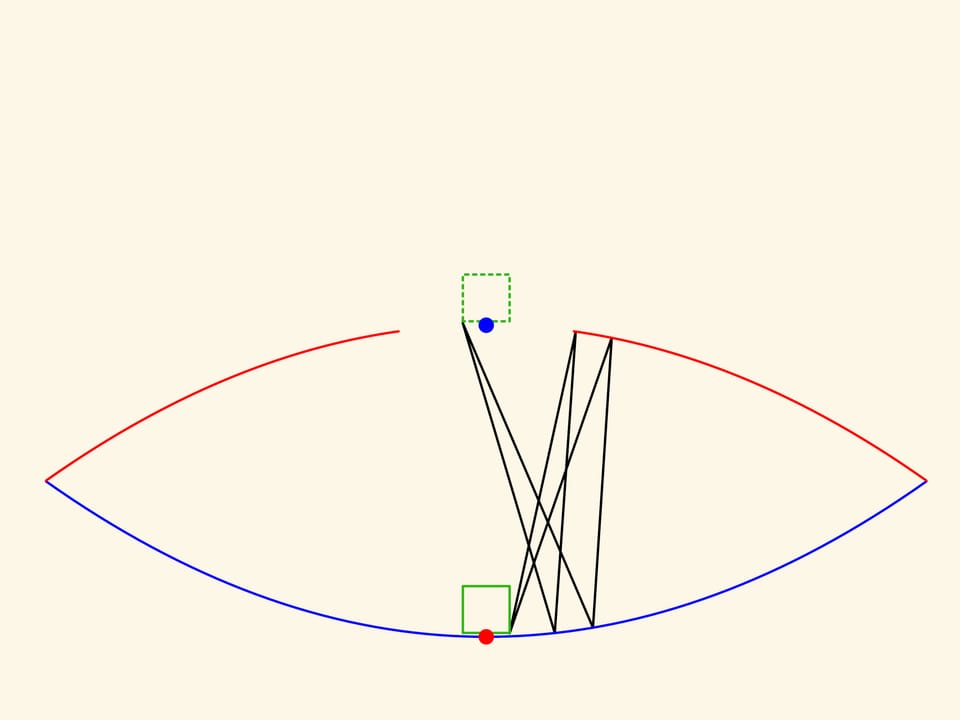
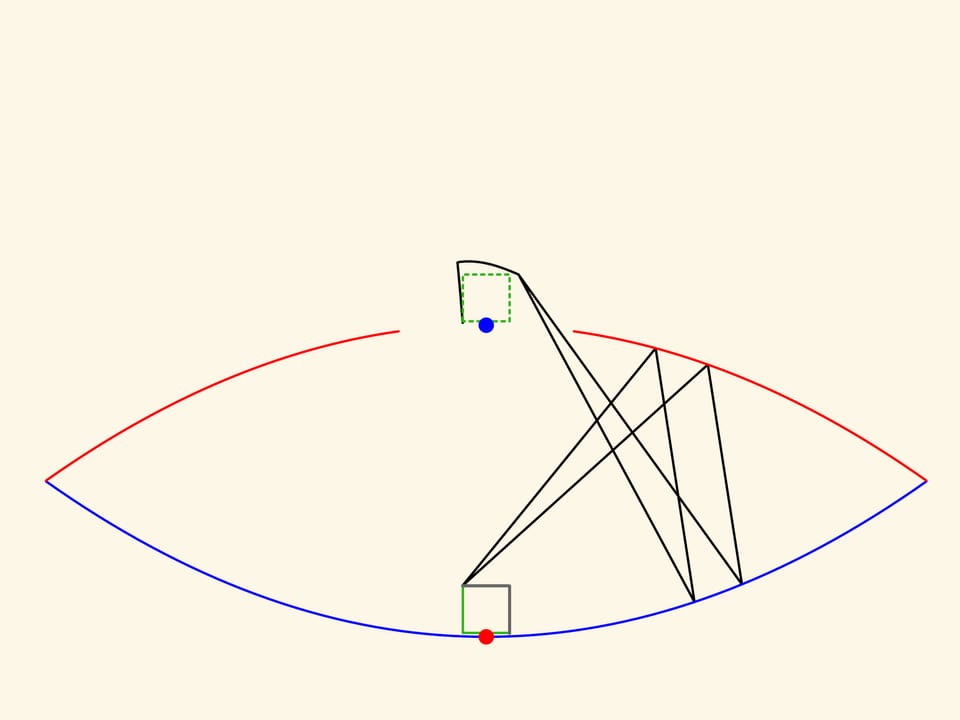
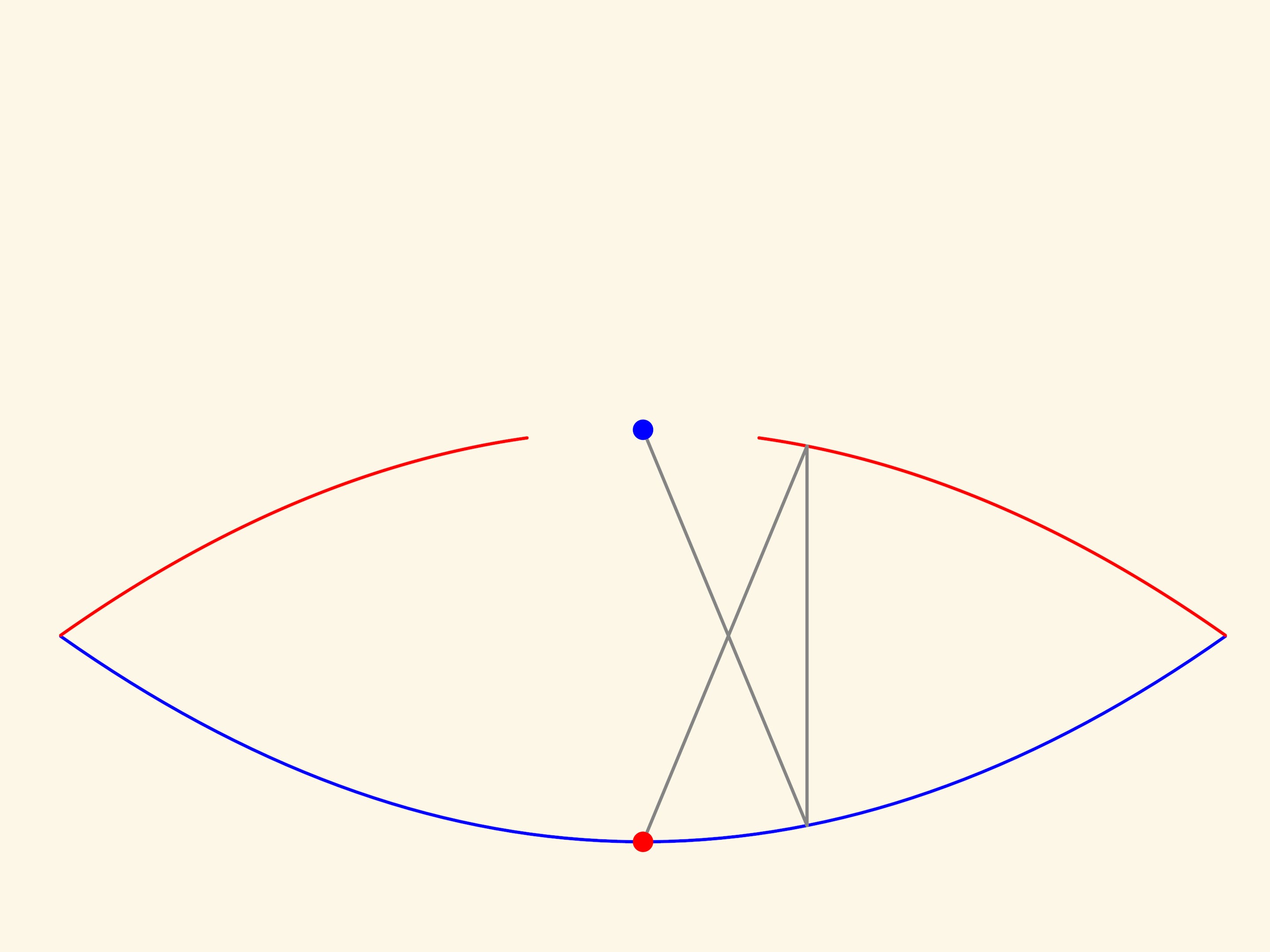
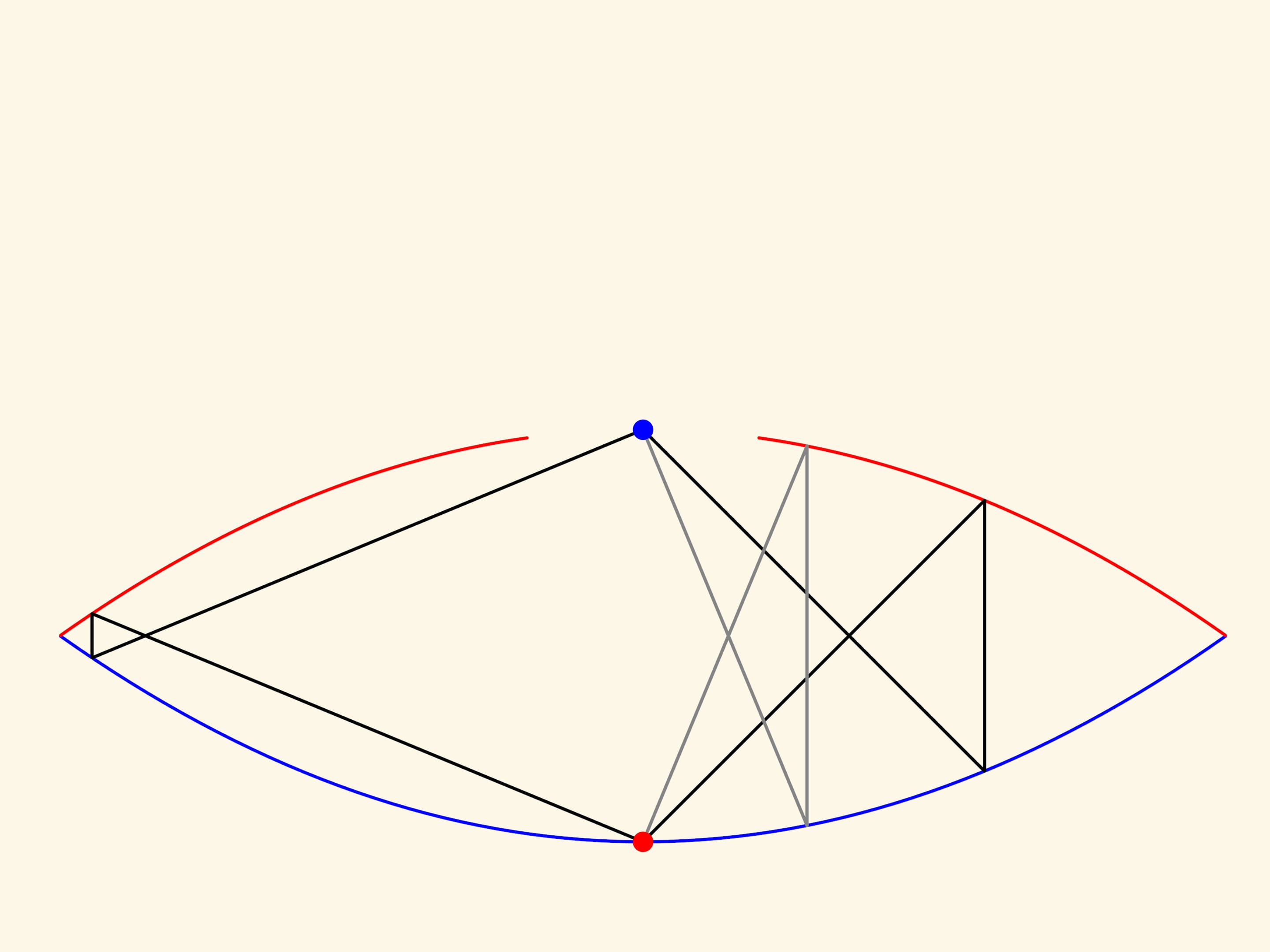
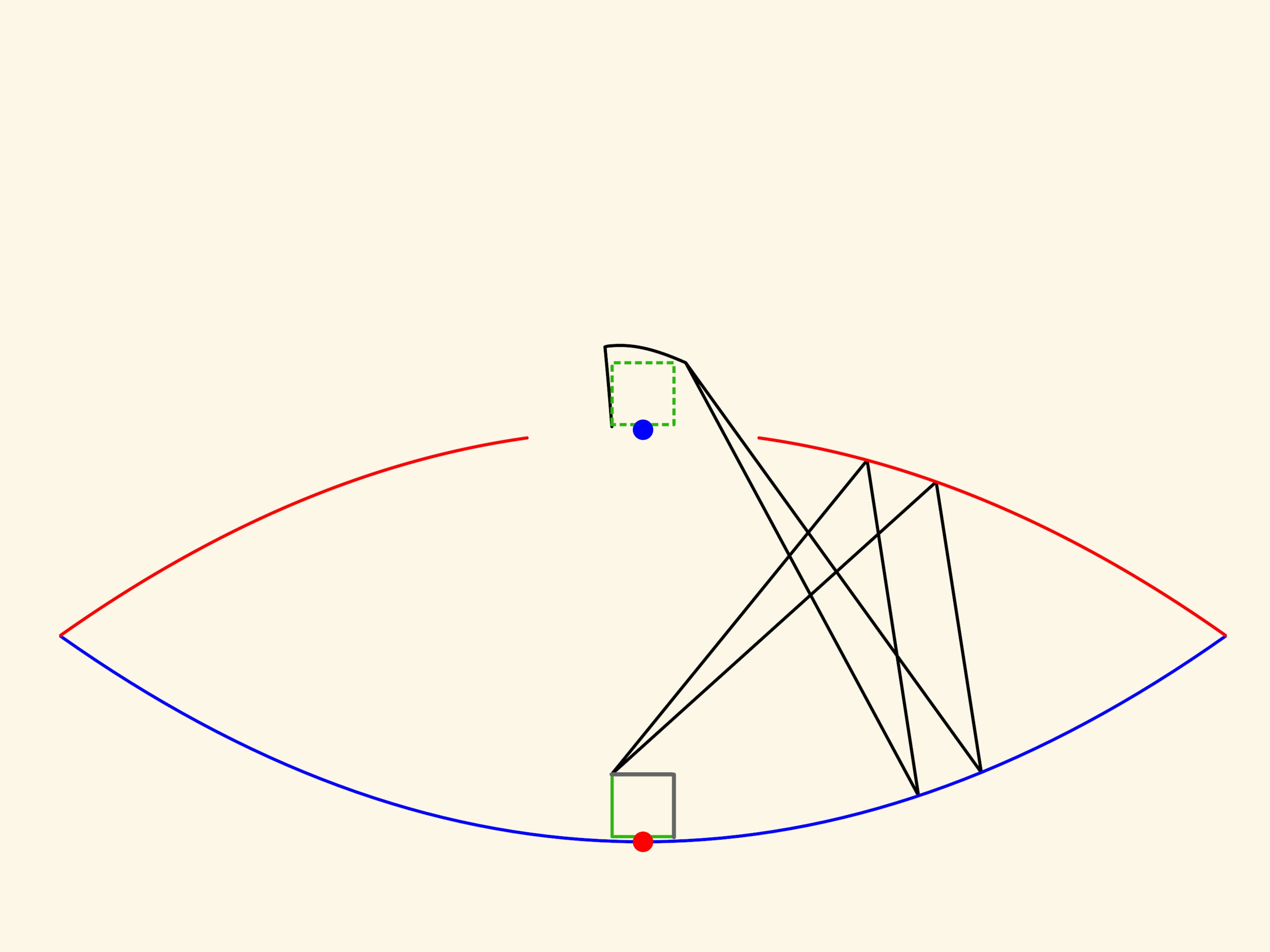
Чтобы построить в данной системе зеркал образ точки, не находящейся в фокусе красной параболы, надо рассмотреть два луча. Место их пересечения — и есть видимое глазом изображение данной точки. Реальный объект не является точкой и не умещается в фокусе — происходят искажения, но они зависят от конкретной рассматриваемой пары лучей. Наш глаз видит много пар и «усредняет». В хорошо сделанной модели любой небольшой предмет отображается довольно реалистично.
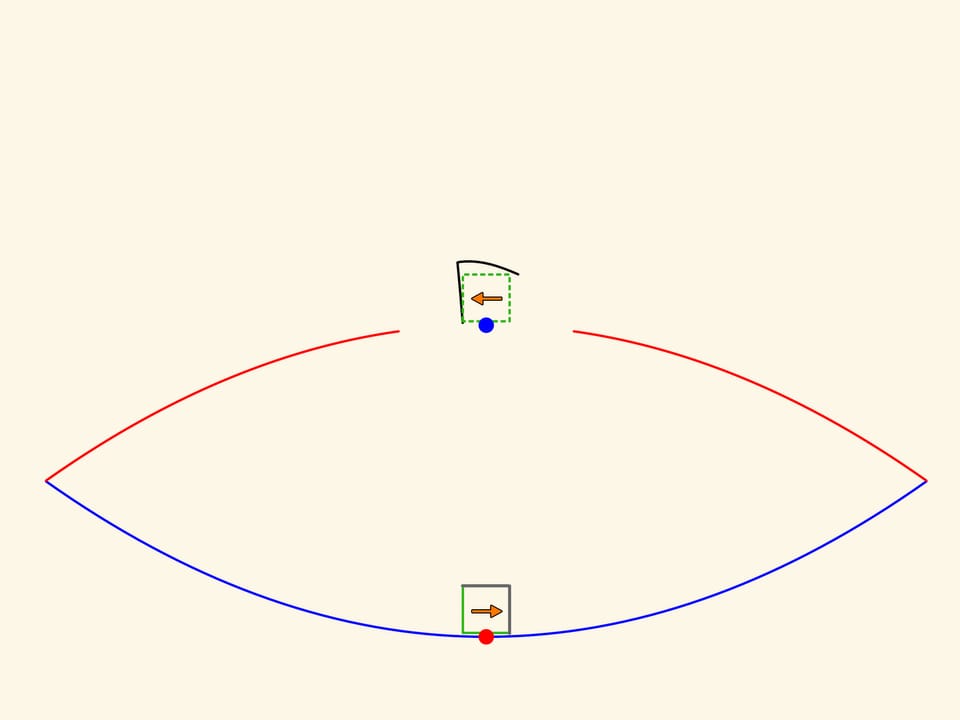
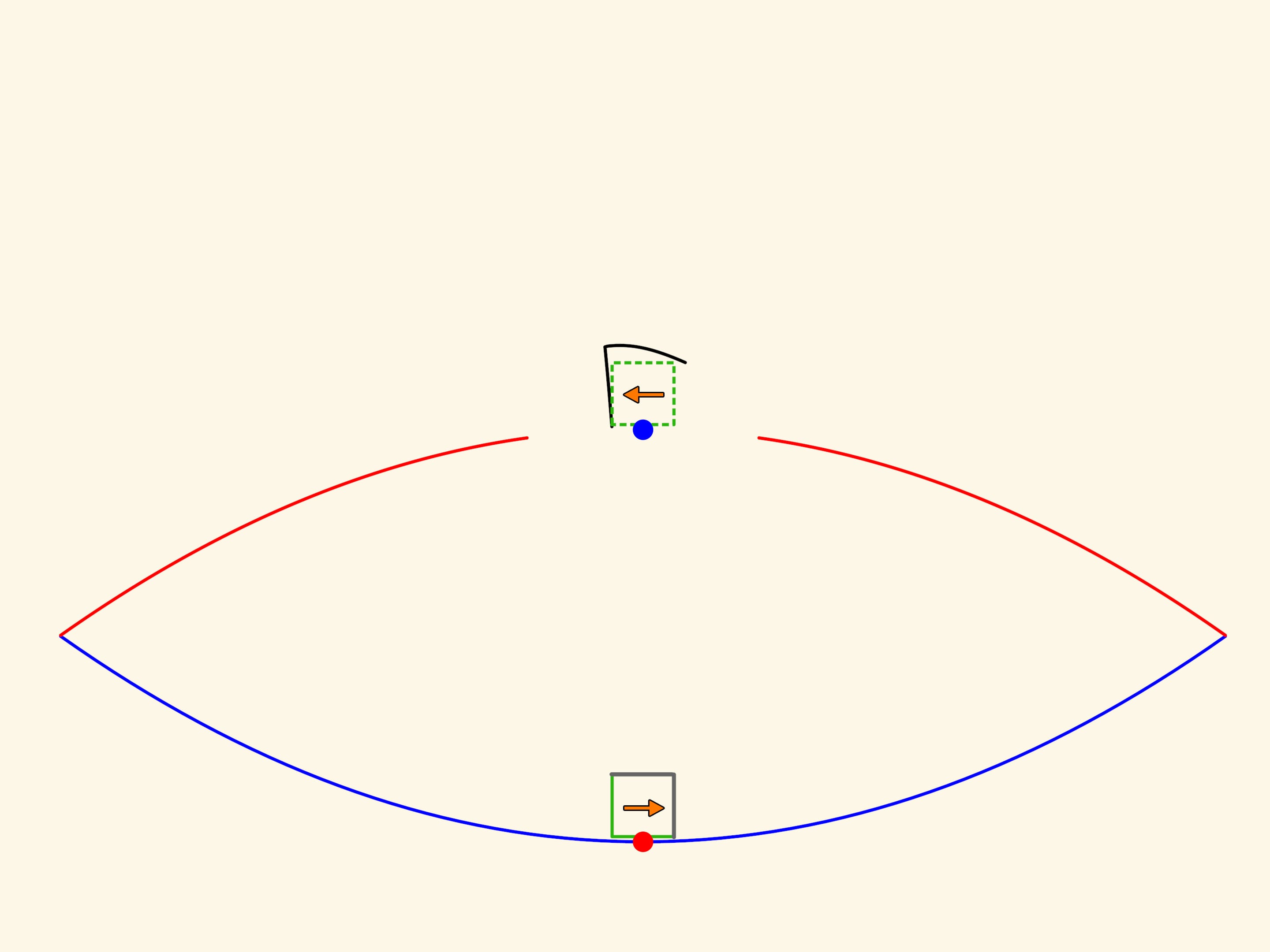
Первый образ объекта, который мы видим над тарелкой, «смотрит» в противоположную сторону относительно объекта. А внимательный экспериментатор может увидеть образы большей кратности и восстановить ход образующих их лучей.
Литература
Параболическая антенна // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — Стр. 46—47, 297—302.