Любое сечение эллипсоида плоскостью — эллипс. А бывает ли сечение, являющееся окружностью?
Если рассматривать эллипсоид вращения — взяли эллипс и провращали вокруг одной из осей, — то, конечно, окружности имеются: в сечении, перпендикулярном оси вращения. Эллипсоиды вращения Архимед ассоциировал со сжатой сферой и называл «сфероид»: вытянутый сфероид, если вращали вокруг большой оси эллипса; сплюснутый сфероид, если вращали вокруг малой оси.
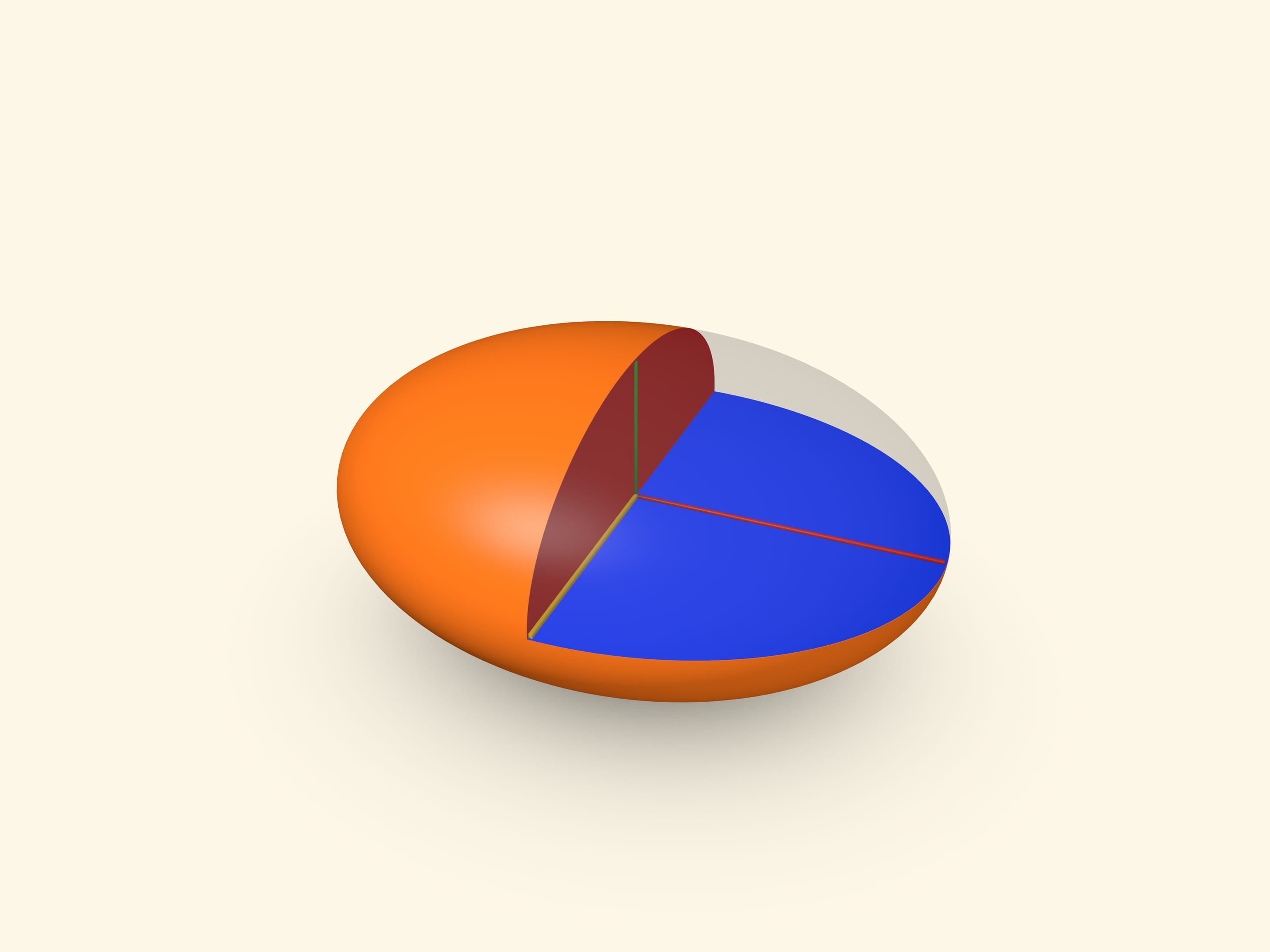
Если сферу сжать по всем трём направлениям, то получается эллипсоид с тремя различными полуосями $a$, $b$, $c$. Каноническое уравнение такого эллипсоида в декартовых координатах, совпадающих с осями сжатия: $\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$. Есть ли на его поверхности окружности?
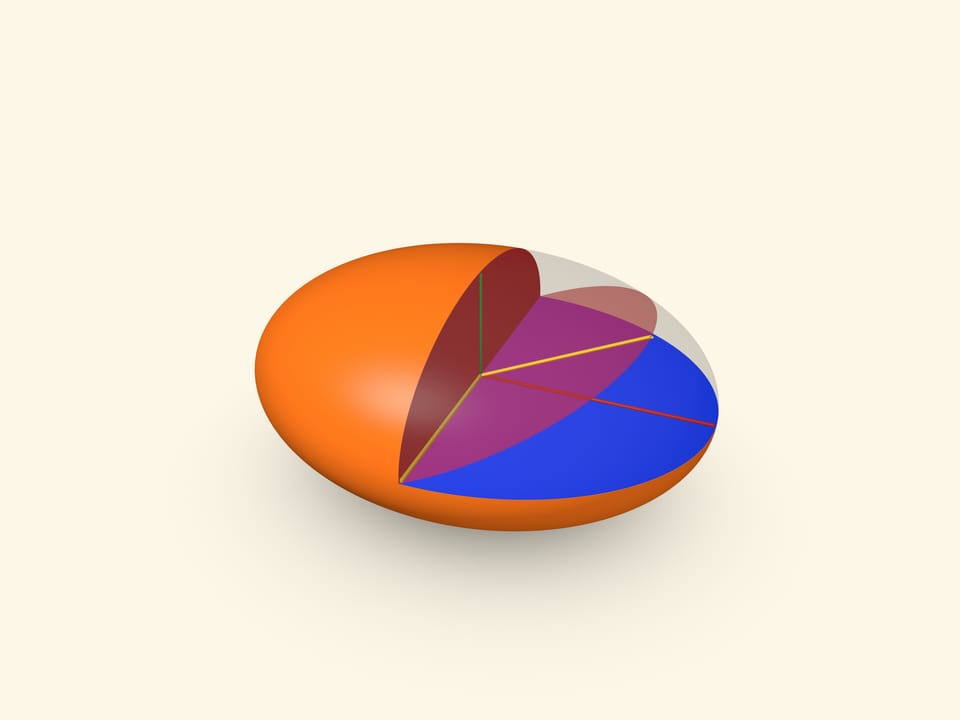
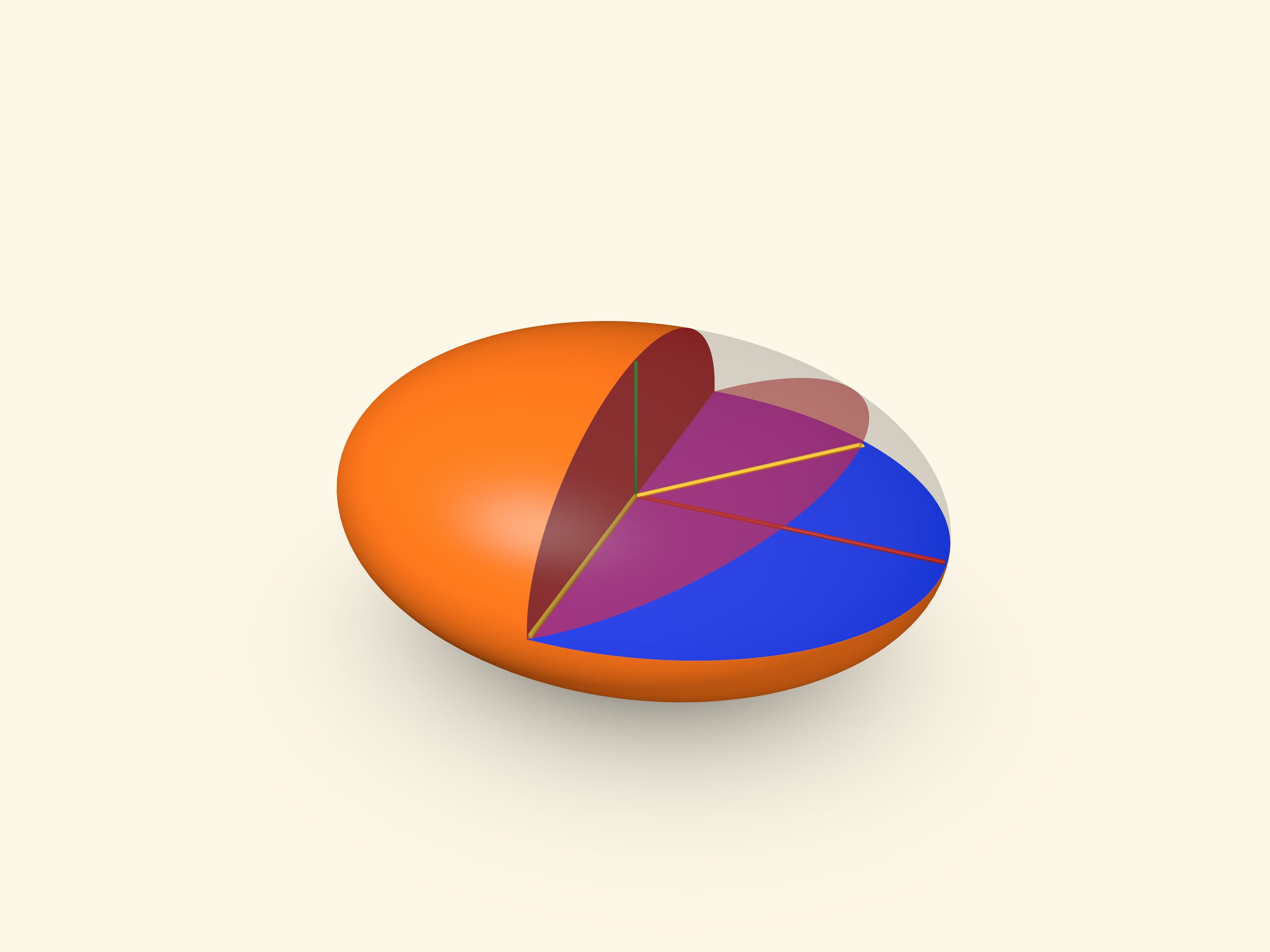
Доказать существование окружностей на поверхности трёхосного эллипсоида можно, воспользовавшись соображениями непрерывности. Любое сечение эллипсоида плоскостью, содержащей среднюю по величине полуось, является эллипсом. Будем наклонять эту плоскость от положения, когда вторая полуось эллипса равна меньшей полуоси эллипсоида, до положения, когда вторая полуось эллипса равна большей полуоси эллипсоида. При каком-то угле наклона полуоси эллипса сравняются — так и получится окружность.
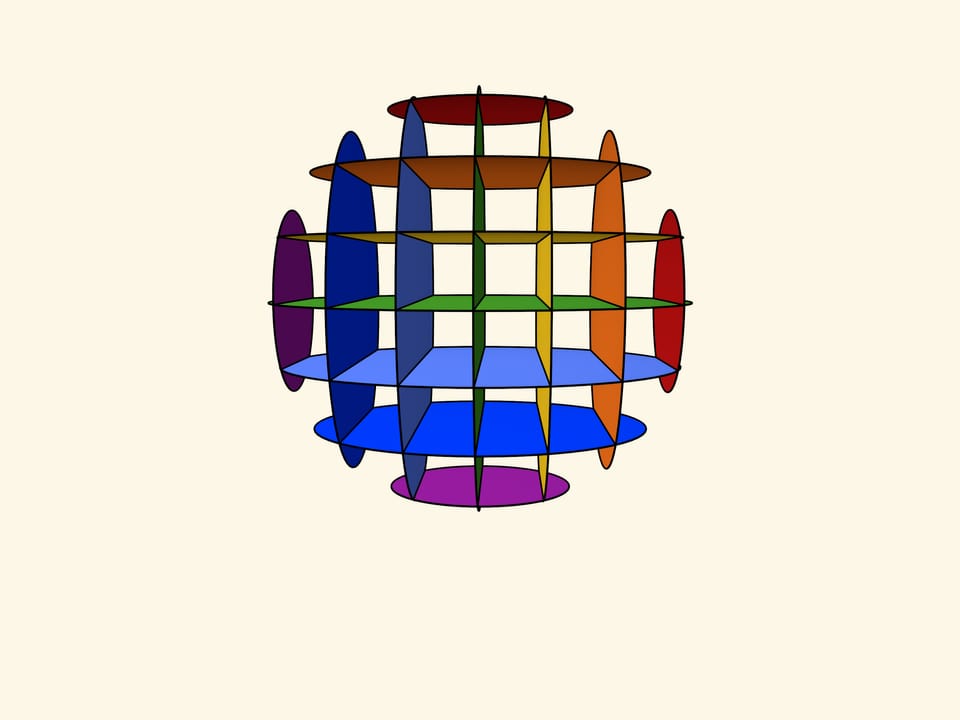
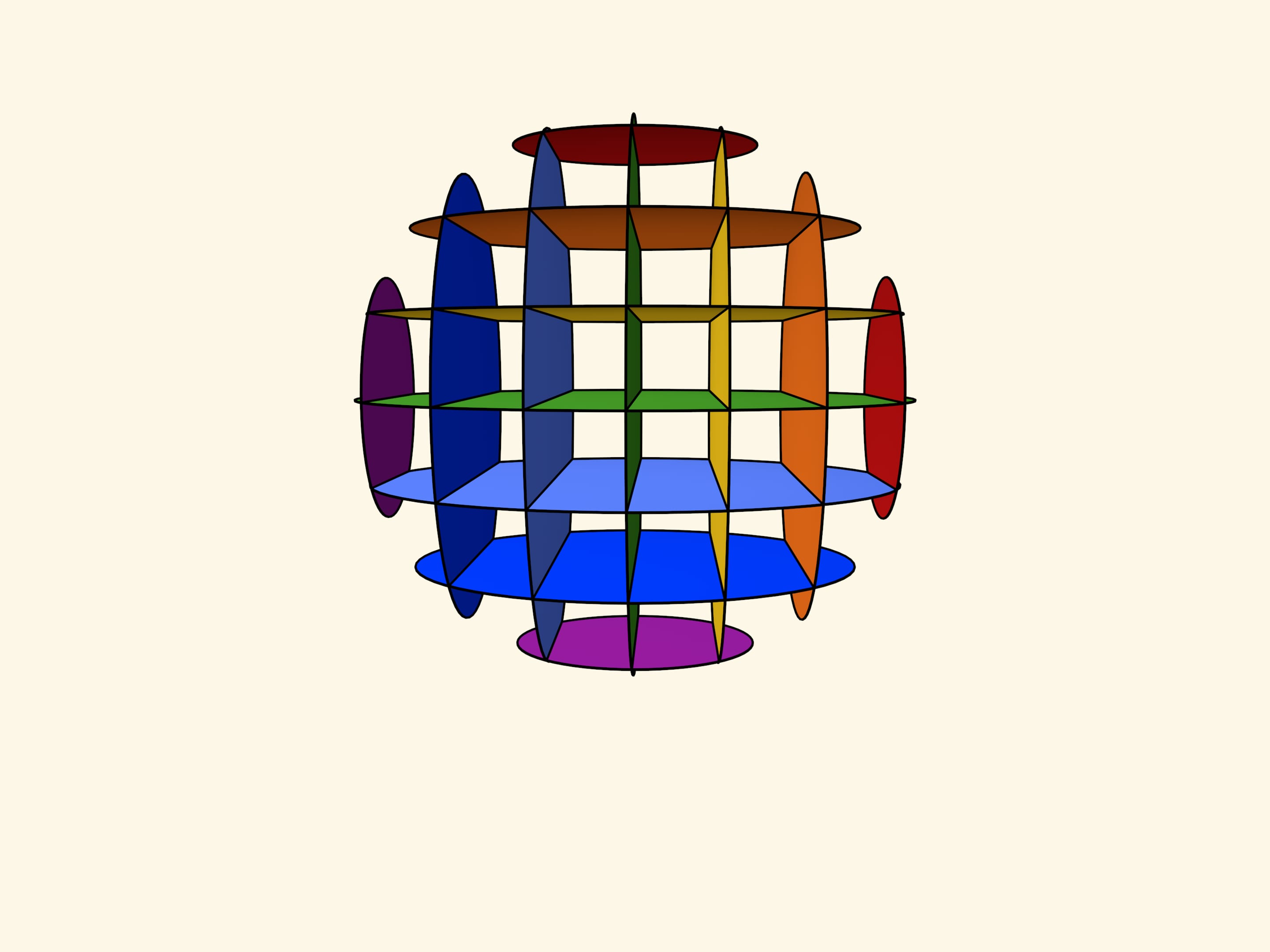
На самом деле на поверхности трёхосного эллипсоида лежит два семейства параллельных друг другу окружностей. Продемонстрировать это можно, сделав наглядную модель из тонкого негнущегося пластика или тонкого, но плотного картона.
Соберём сферу из пластин. (Идея соединения пластин с помощью прорезей уже использовалась в моделе Гиперболический параболоид: модель из картона.) Такое соединение позволяет «складывать» модель. При складывании сфера переходит в эллипсоид, но пластины в каждом из двух семейств остаются параллельными друг другу.
Границы пластин-кругов и есть окружности, лежащие на поверхности эллипсоида. И плоскости окружностей в каждом из двух семейств параллельны друг другу.
Литература
Гильберт Д., Кон‐Фоссен С. Наглядная геометрия. — М.—Л.: ОНТИ, 1936. — [Переиздания: 1951, 2004]. — [Глава 1 «Простейшие кривые и поверхности», § 3 «Поверхности второго порядка»].
Другие модели раздела «Пластинчатые конструкции»
