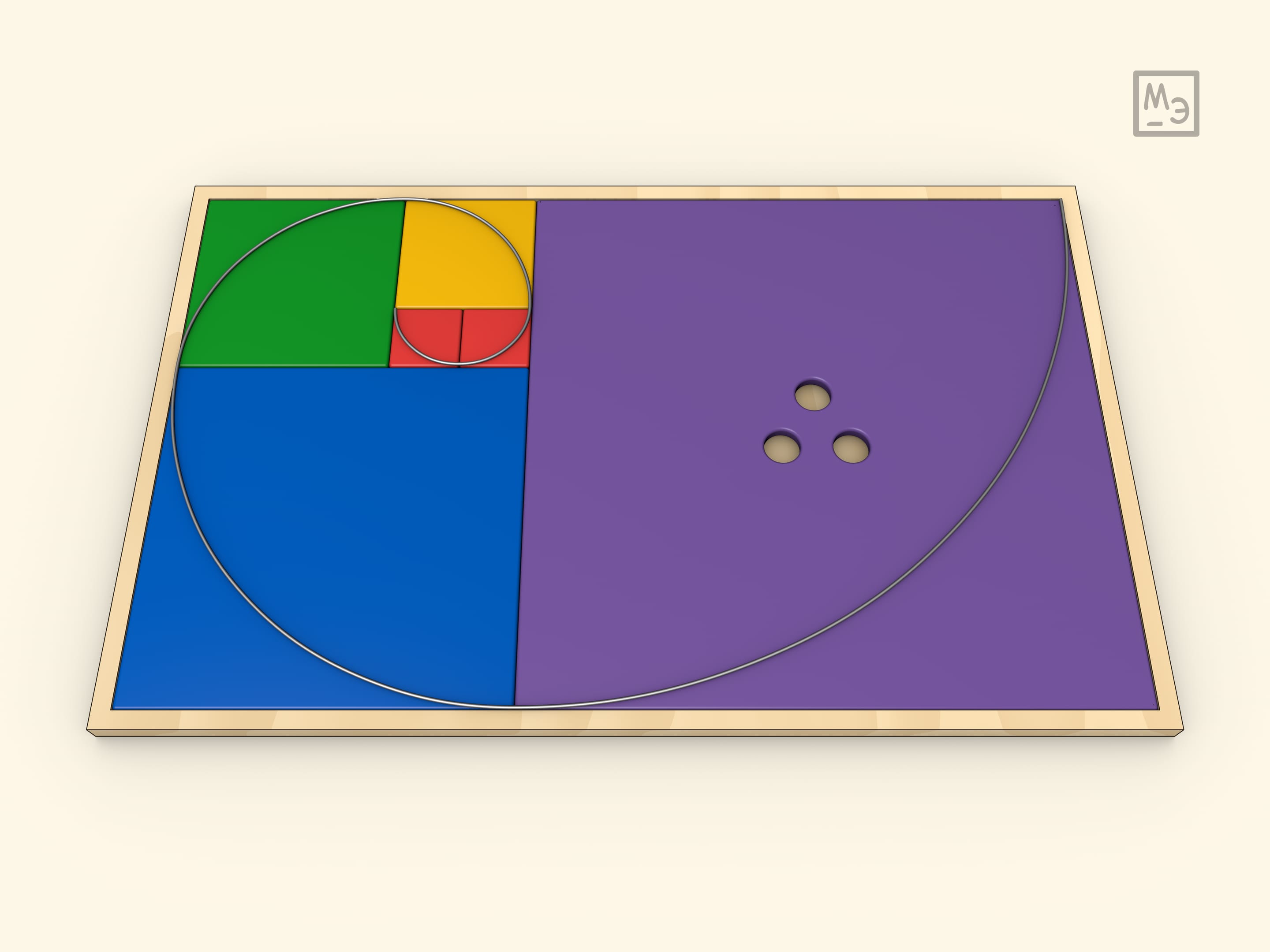
Рекуррентную формулу $F_n=F_{n-1}+F_{n-2}$, задающую при начальных условиях $F_0=1$, $F_1=1$ последовательность чисел Фибоначчи, можно представить геометрически. Стоит лишь правильно укладывать квадраты со сторонами $1$, $1$, $2$, $3$, $5$, $8$, $12$, …, прикладывая следующий квадрат к сторонам двух предыдущих.
Такая укладка не единственна, а одна из возможных — когда квадраты уложены «по спирали». Спиральную укладку можно продолжать до бесконечности: укладывание по спирали — один из стандартных способов замощения плоскости многоугольниками.
Уложенные квадраты можно дополнить проволочной спиралью.
Отметим, что бывают две похожие друг на друга спирали. Самая математическая — логарифмическая спираль с параметром, зависящим от золотого сечения $\varphi$. Приближением к ней является спираль Фибоначчи, представленная на картинке, или «обратная» к ней спираль Дюрера. Она составлена из четвертинок окружностей «вписанных» в квадраты — радиус равен стороне квадрата, а центр находится в вершине. Когда строят «от малого к большому» эту спираль называют спиралью Дюрера, когда «разматывают» — спиралью Фибоначчи.
Литература
Исчезающая клетка и числа Фибоначчи
Филлотаксис // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — Стр. 78, 318.
Другие модели раздела «Числа и их свойства»
