Устройство для рисования эллипсов, называемое эллипсограф да Винчи, современные эффектные видеоролики, находимые по названию Trammel of Archimedes, объединяет и объясняет теорема из планиметрии — теорема Коперника.
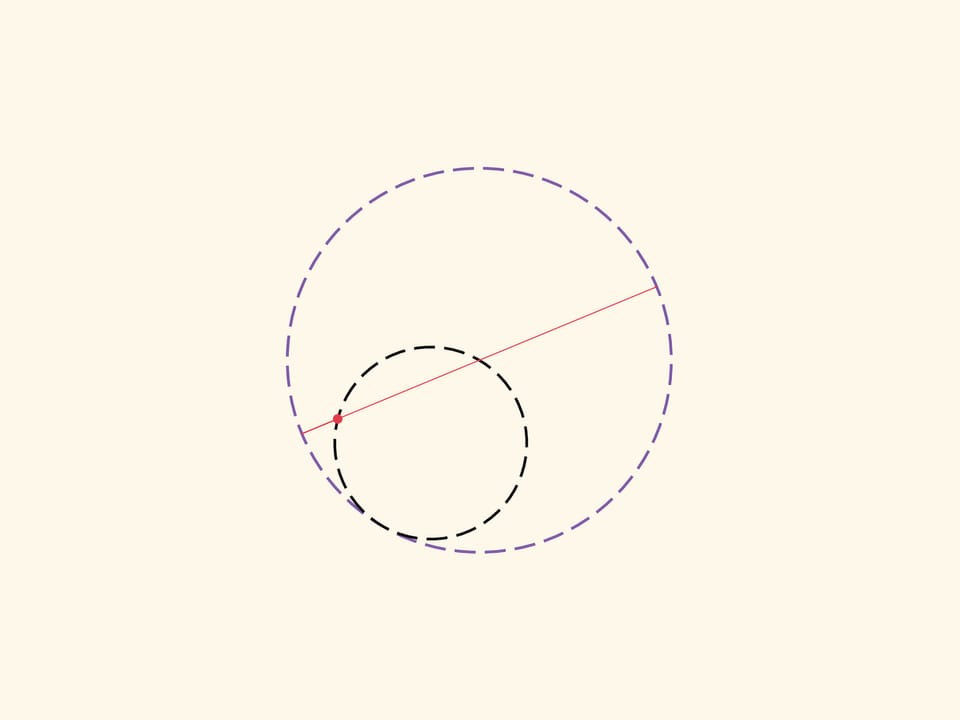
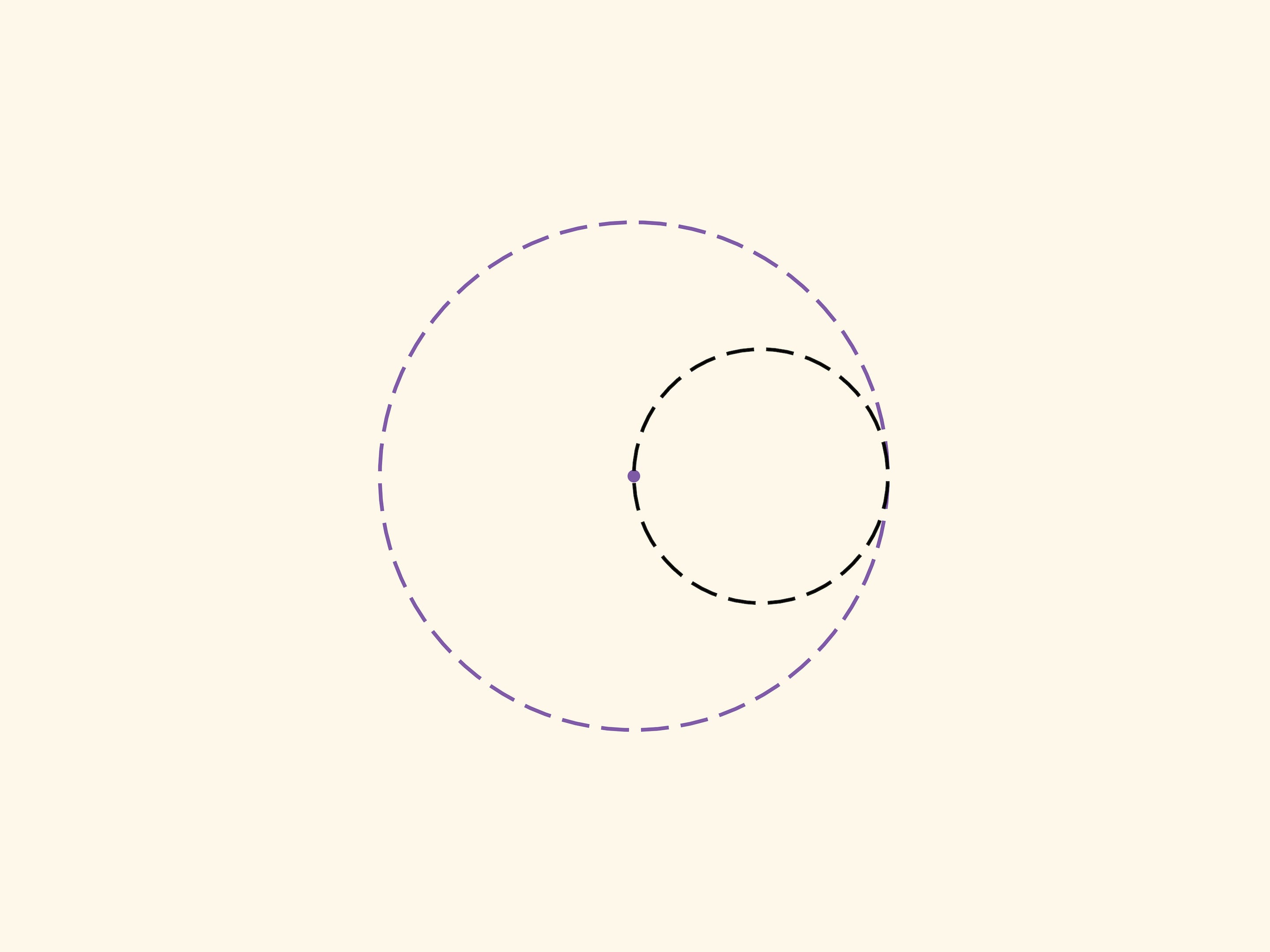
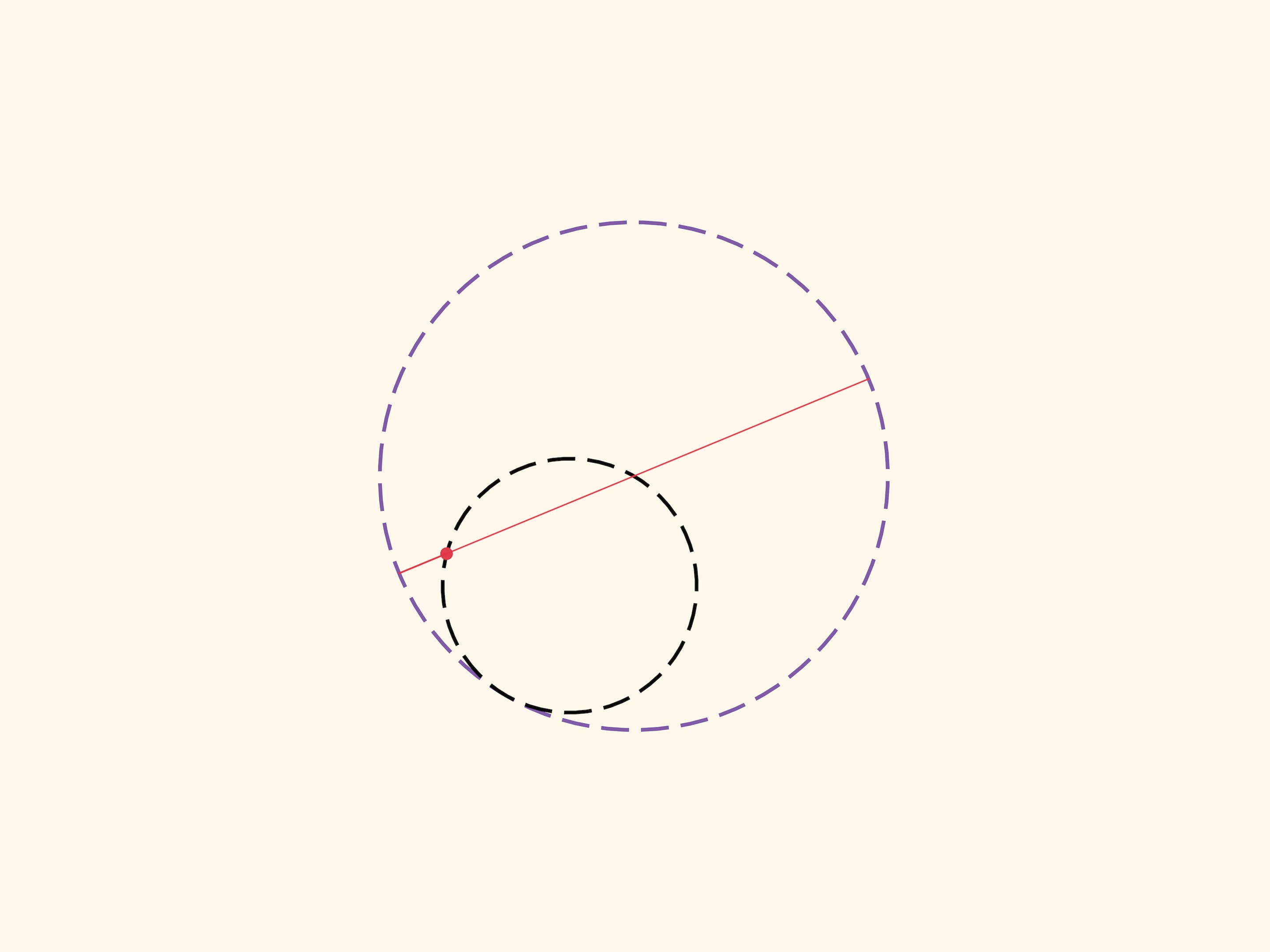
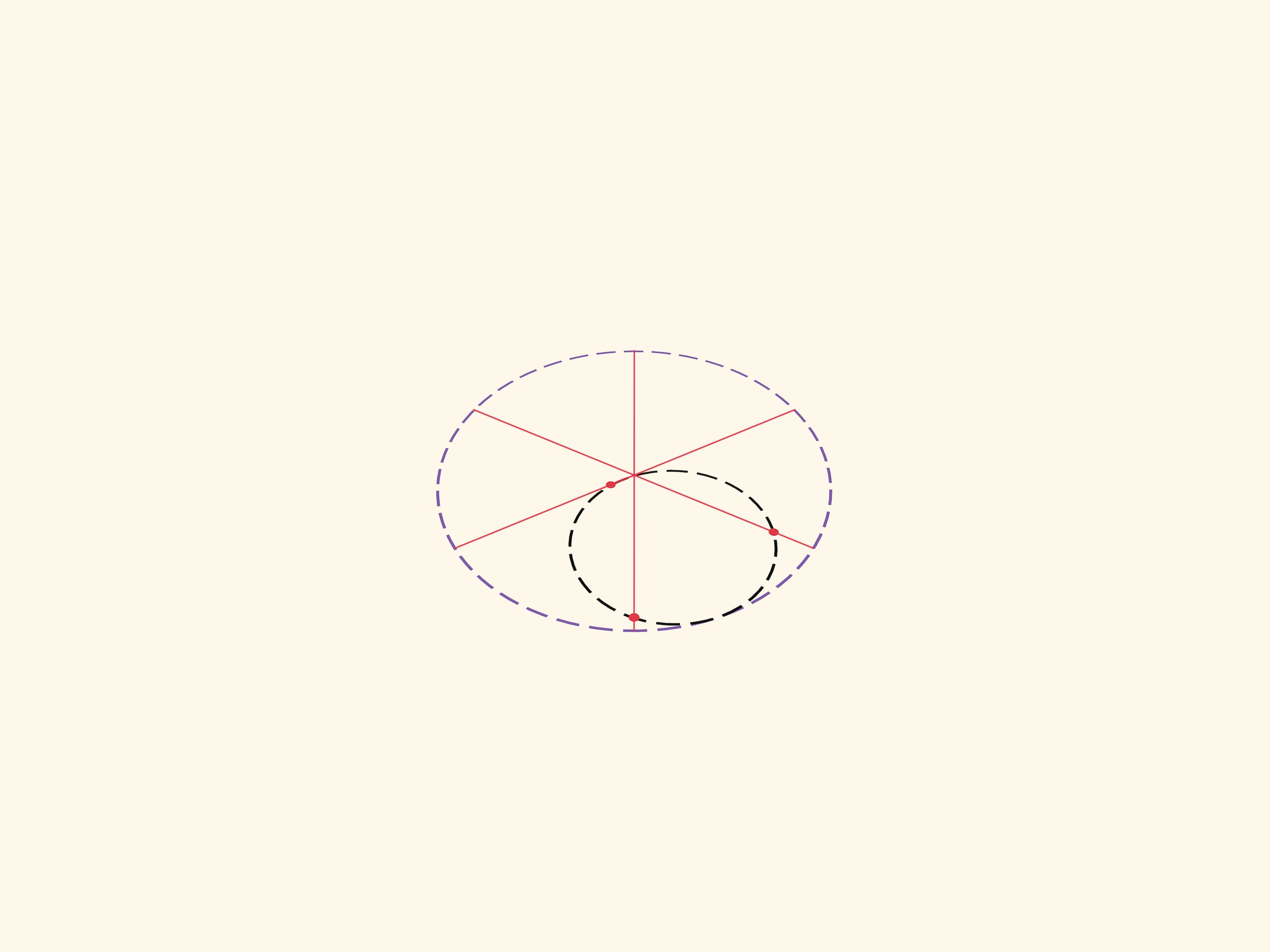
Окружность внутренним образом касается окружности вдвое большего радиуса и катится по ней без проскальзывания. Какую траекторию описывает фиксированная точка маленькой подвижной окружности? Оказывается, это будет отрезок — диаметр большой окружности. В этом и состоит утверждение, называемое теоремой Коперника.
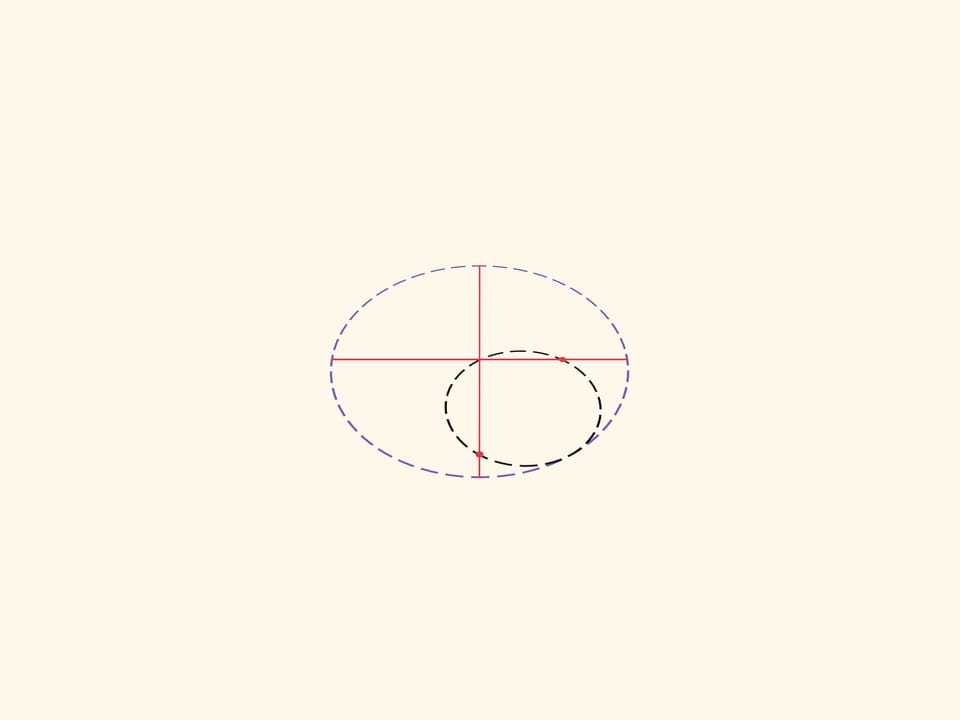
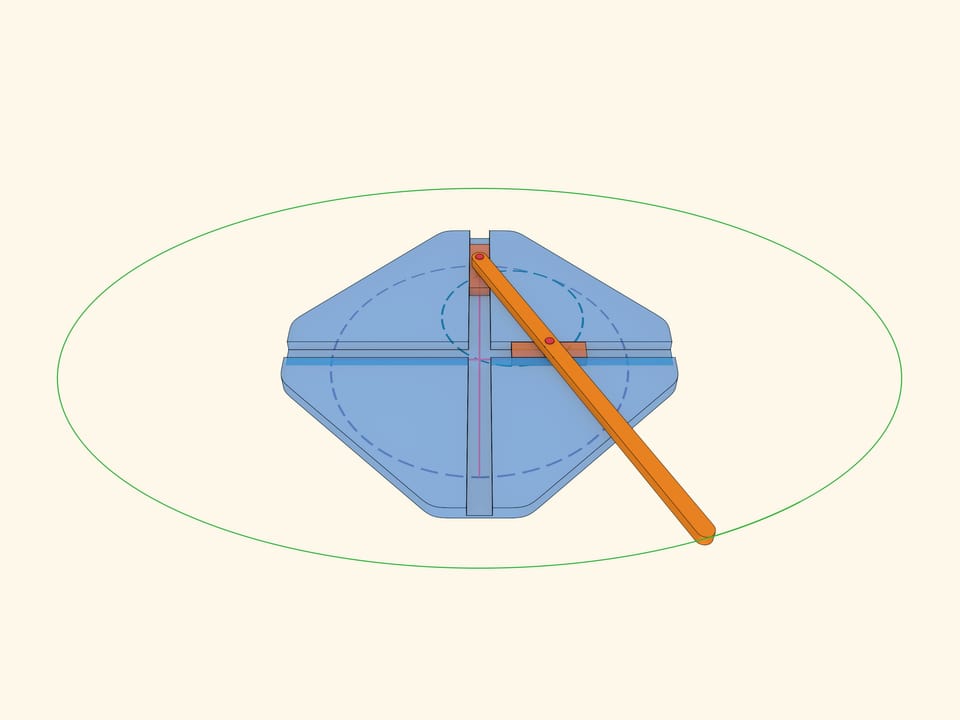
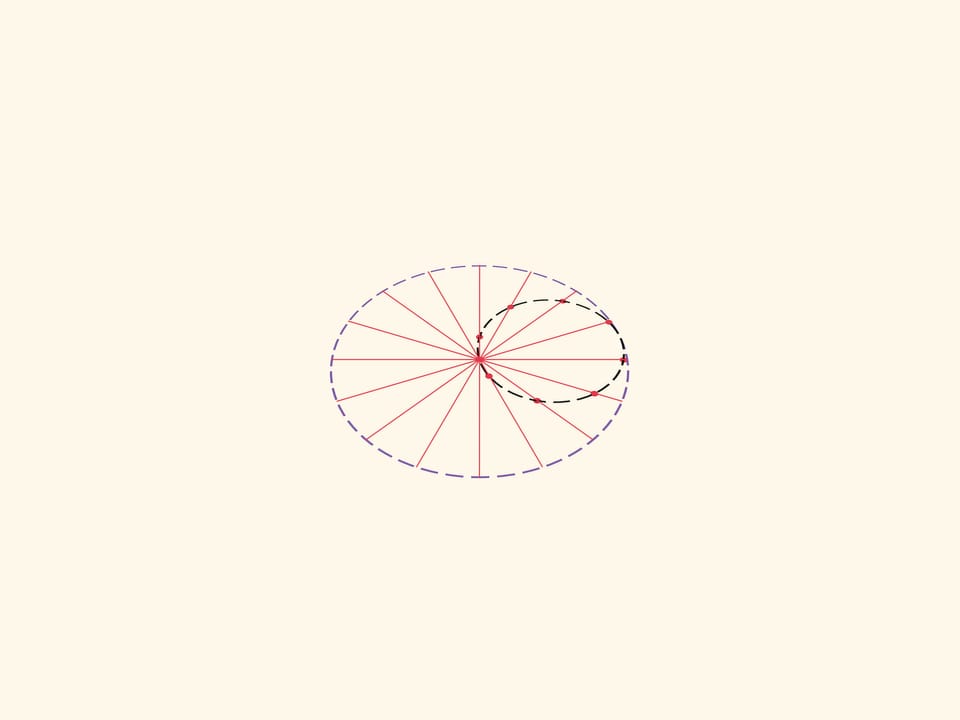
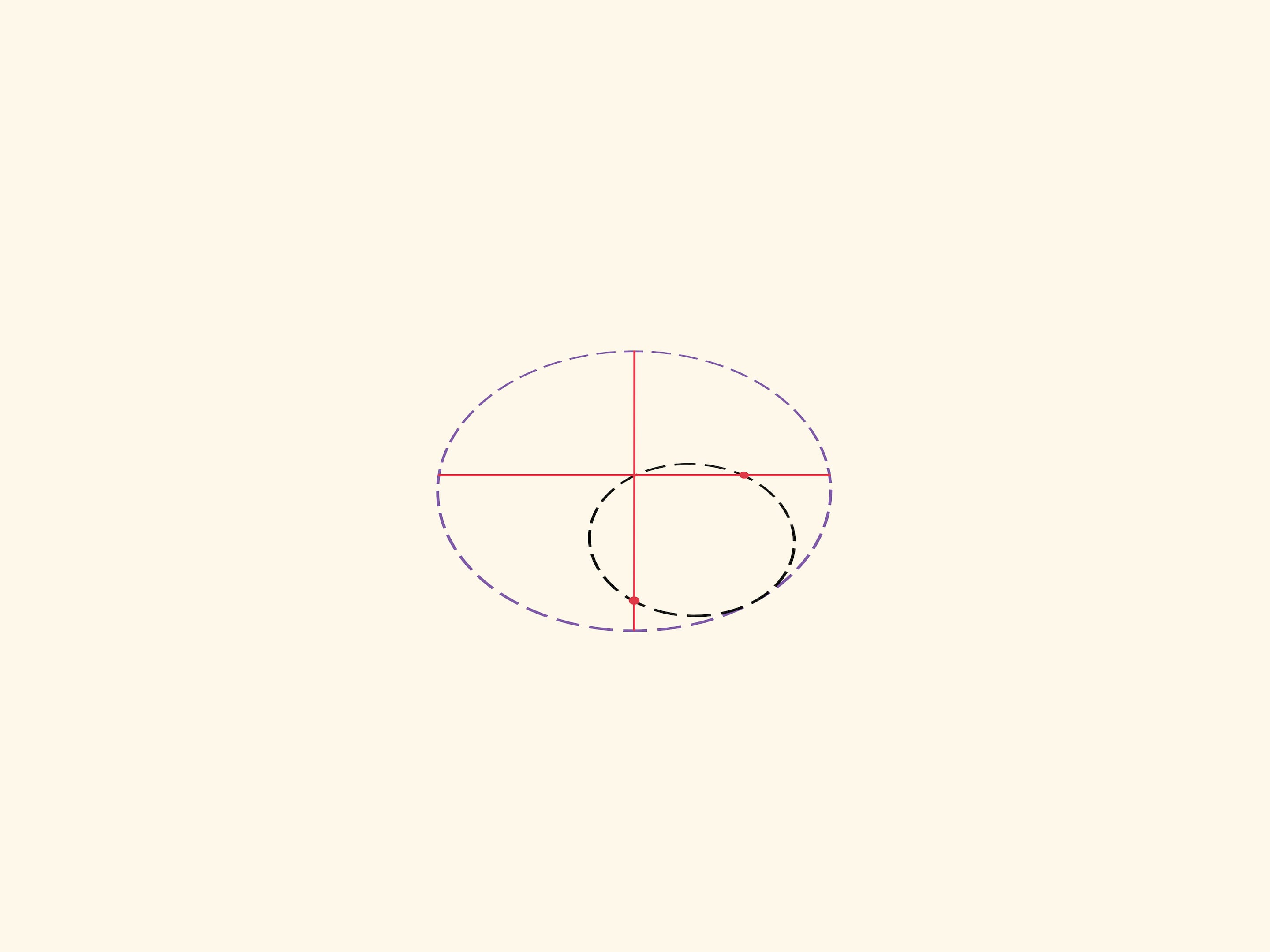
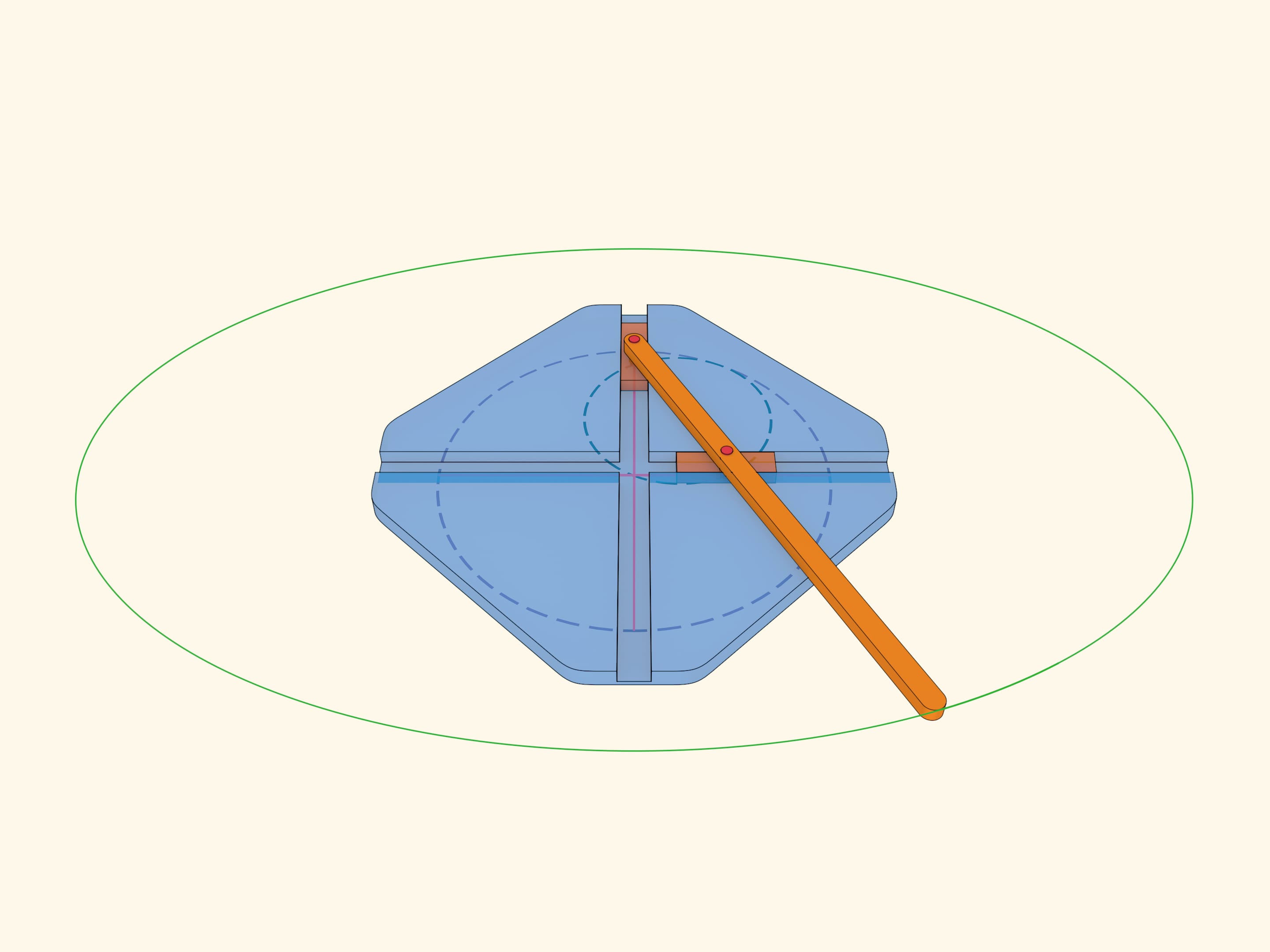
Каждая конкретная точка катящейся окружности рисует свой диаметр. Две диаметрально противоположные точки маленькой окружности нарисуют два перпендикулярных диаметра большой окружности. Механизм для построения эллипсов, основанный на этой идее можно встретить уже в работах Леонардо да Винчи. Любая точка коромысла, а не только его конец, описывает эллипс. Для точек между ползунами это модификация задачи «Котёнок на лестнице». Если представить плоскость, связанную с коромыслом, то и любая точка этой плоскости будет описывать эллипс над плоскостью-основанием.
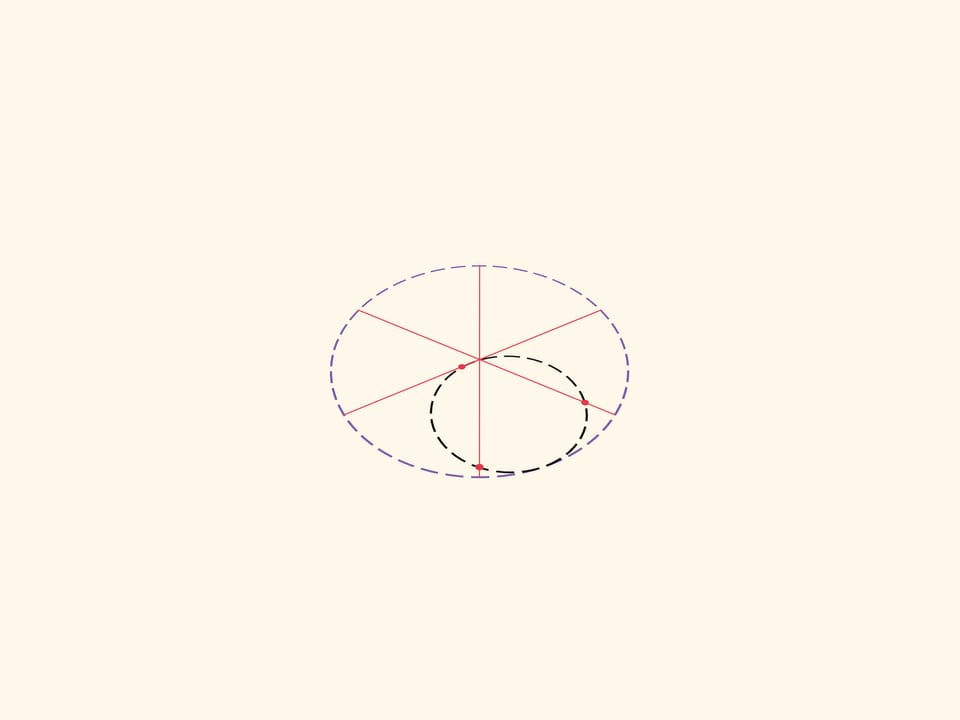
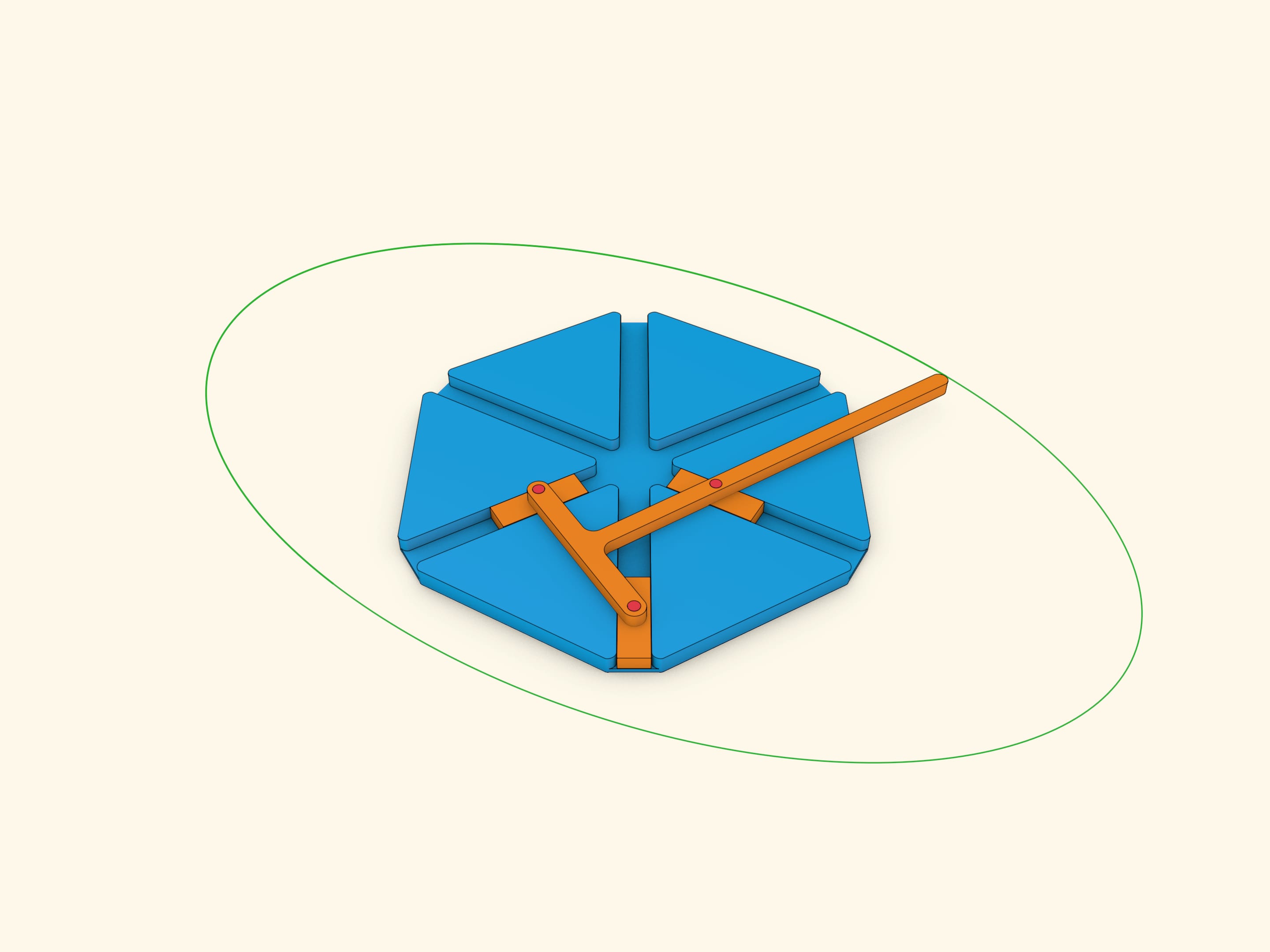
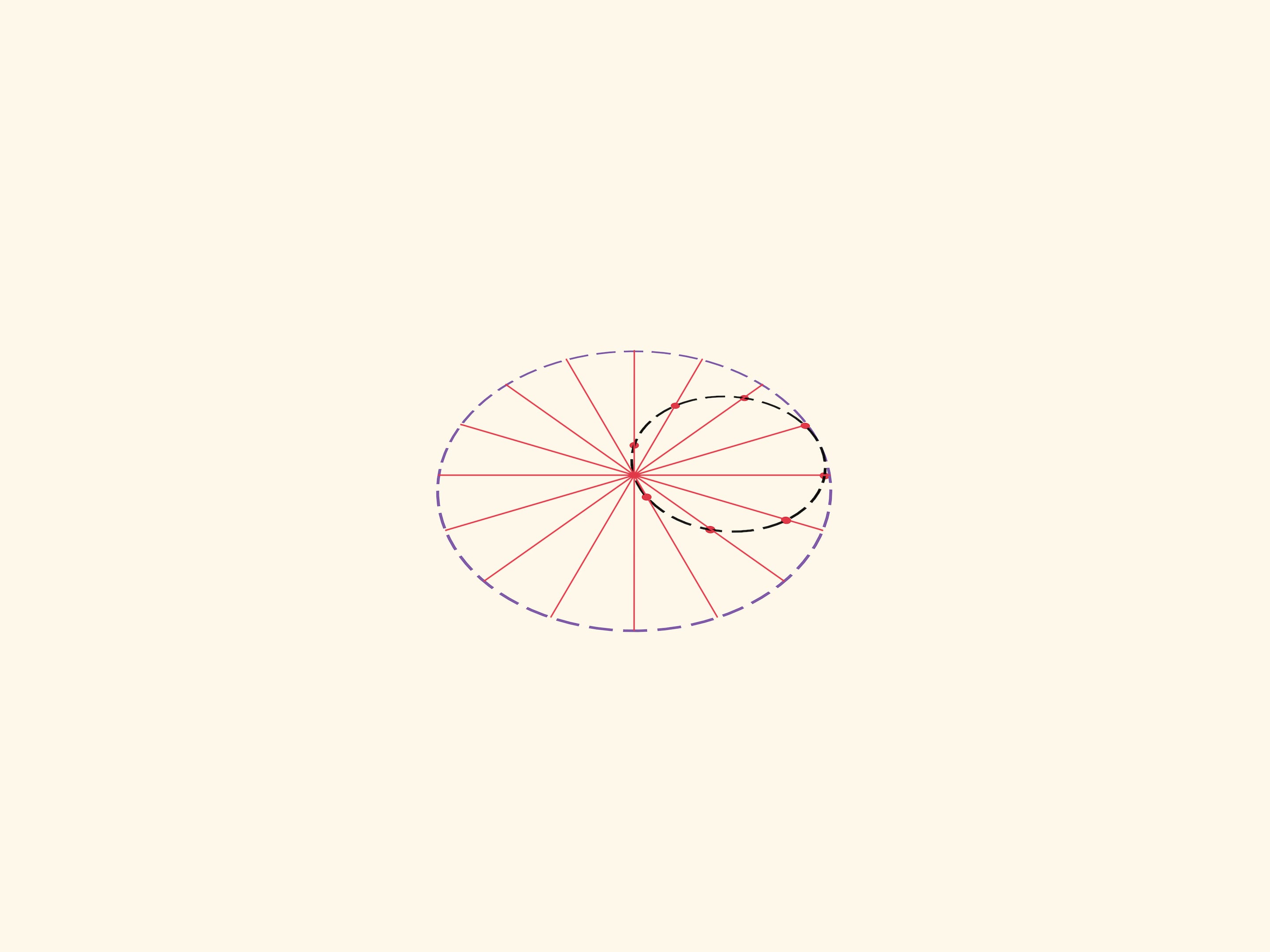
Количество точек на малой окружности и, соответственно, количество ползунов можно варьировать. Три точки на маленькой окружности — три диаметра, три ползуна.
Теорема Коперника является и математической основой завораживающих видеороликов, где несколько шариков эффектно катаются внутри круга по прямым и не сталкиваются.
Литература
Васильев Н. Б., Гутенмахер В. Л. Прямые и кривые. — 2-е изд. — М. : Наука, 1978. — [Интернет-версия].
Котёнок на лестнице // Математические этюды.
Дробление камней в почках // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — Стр. 48—49, 302—303.