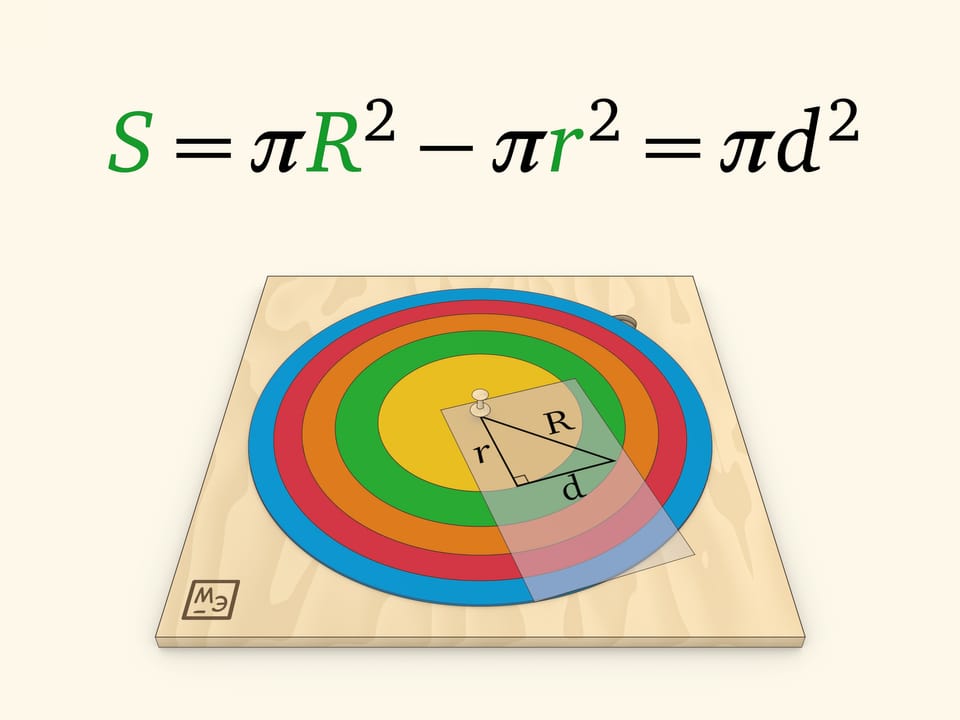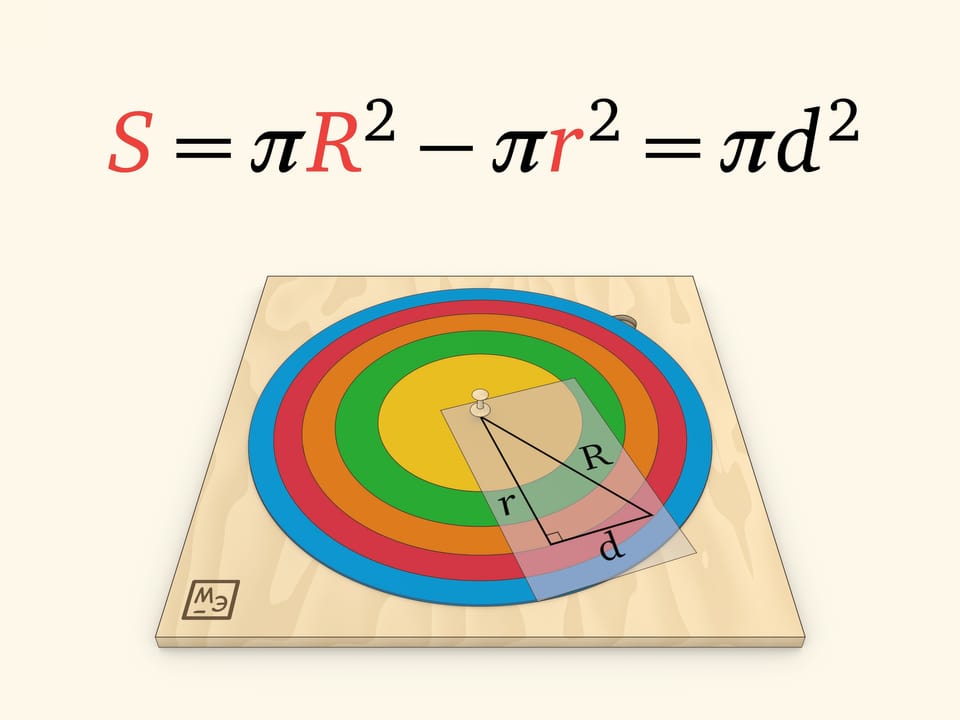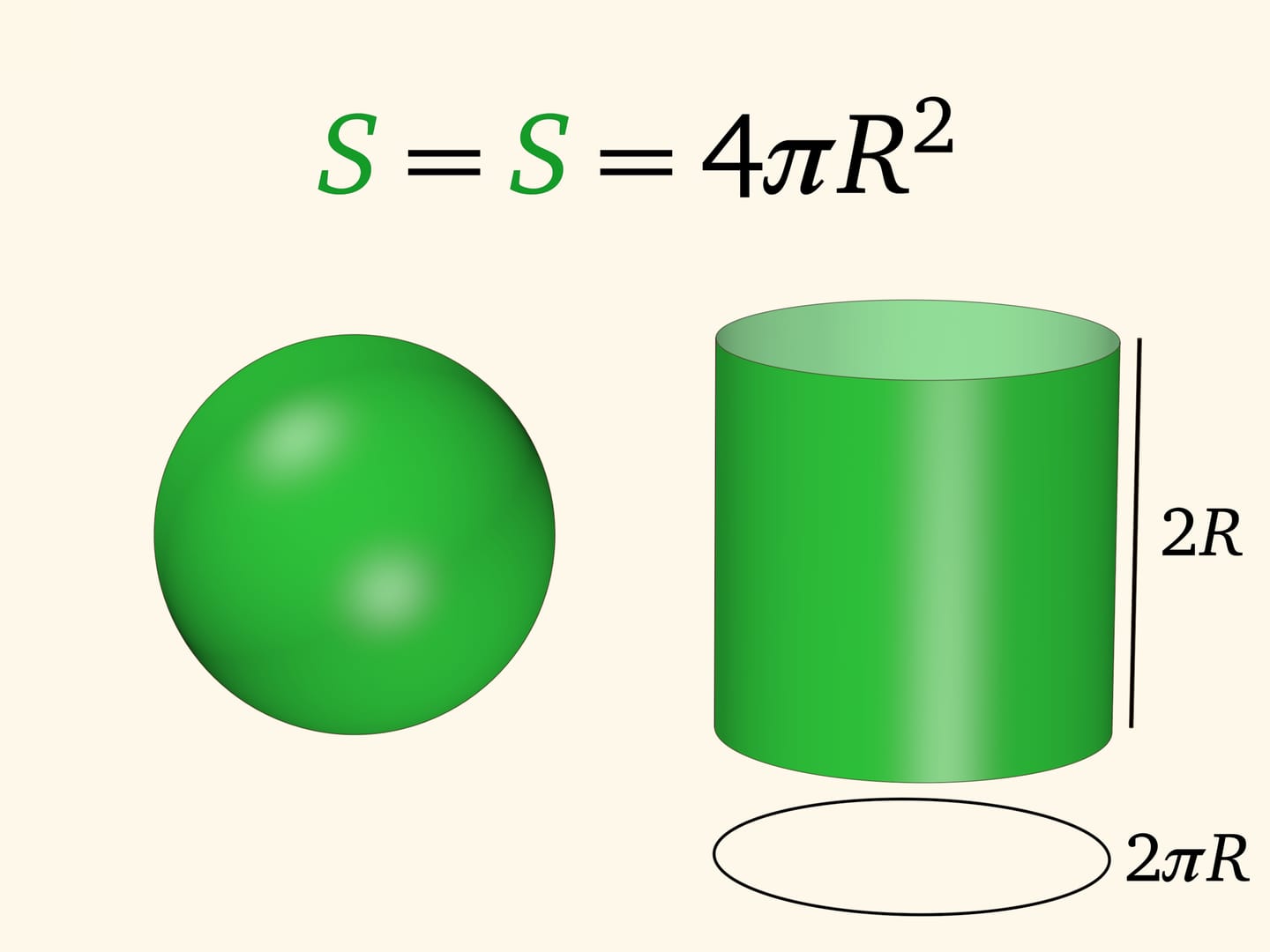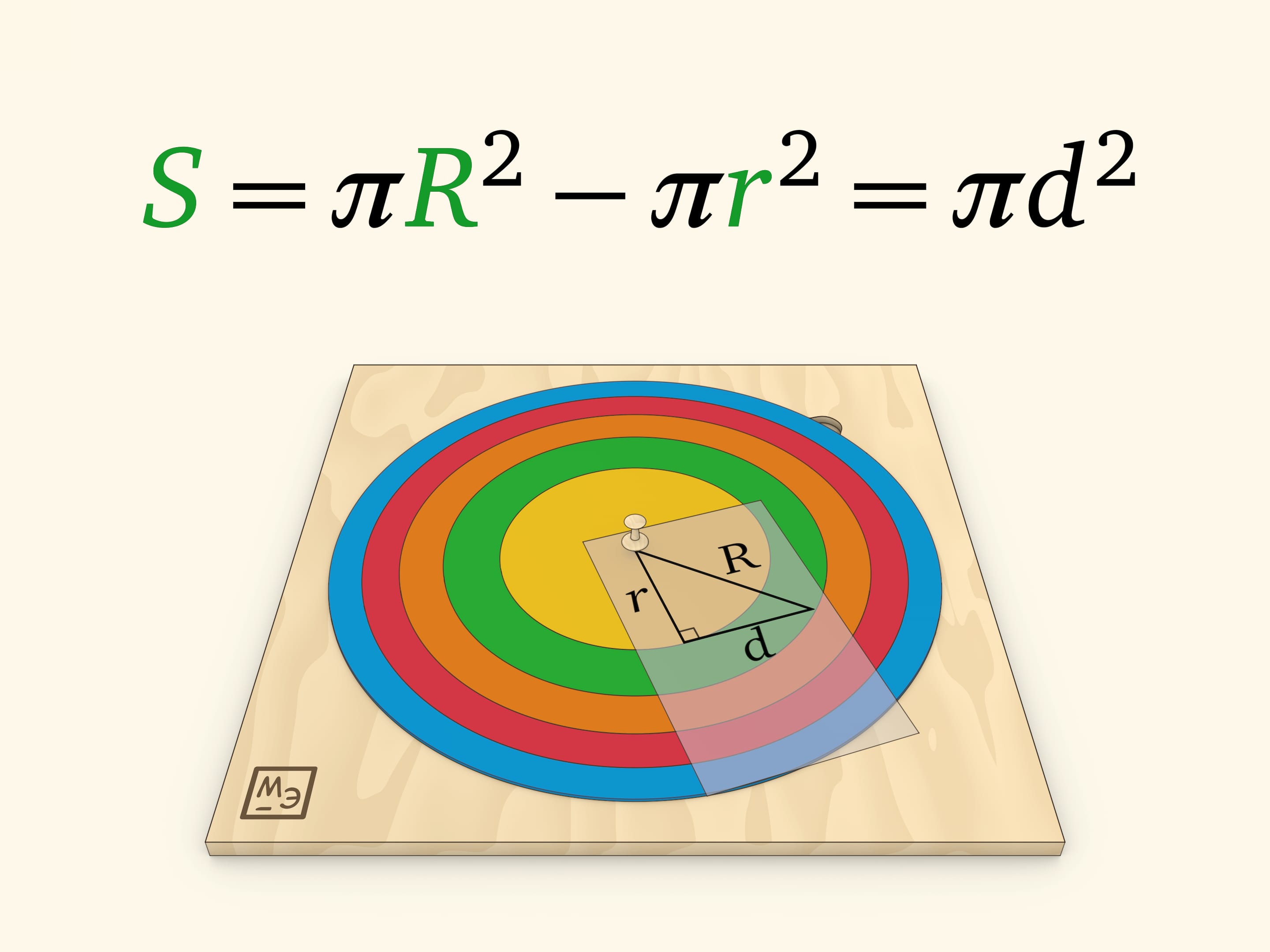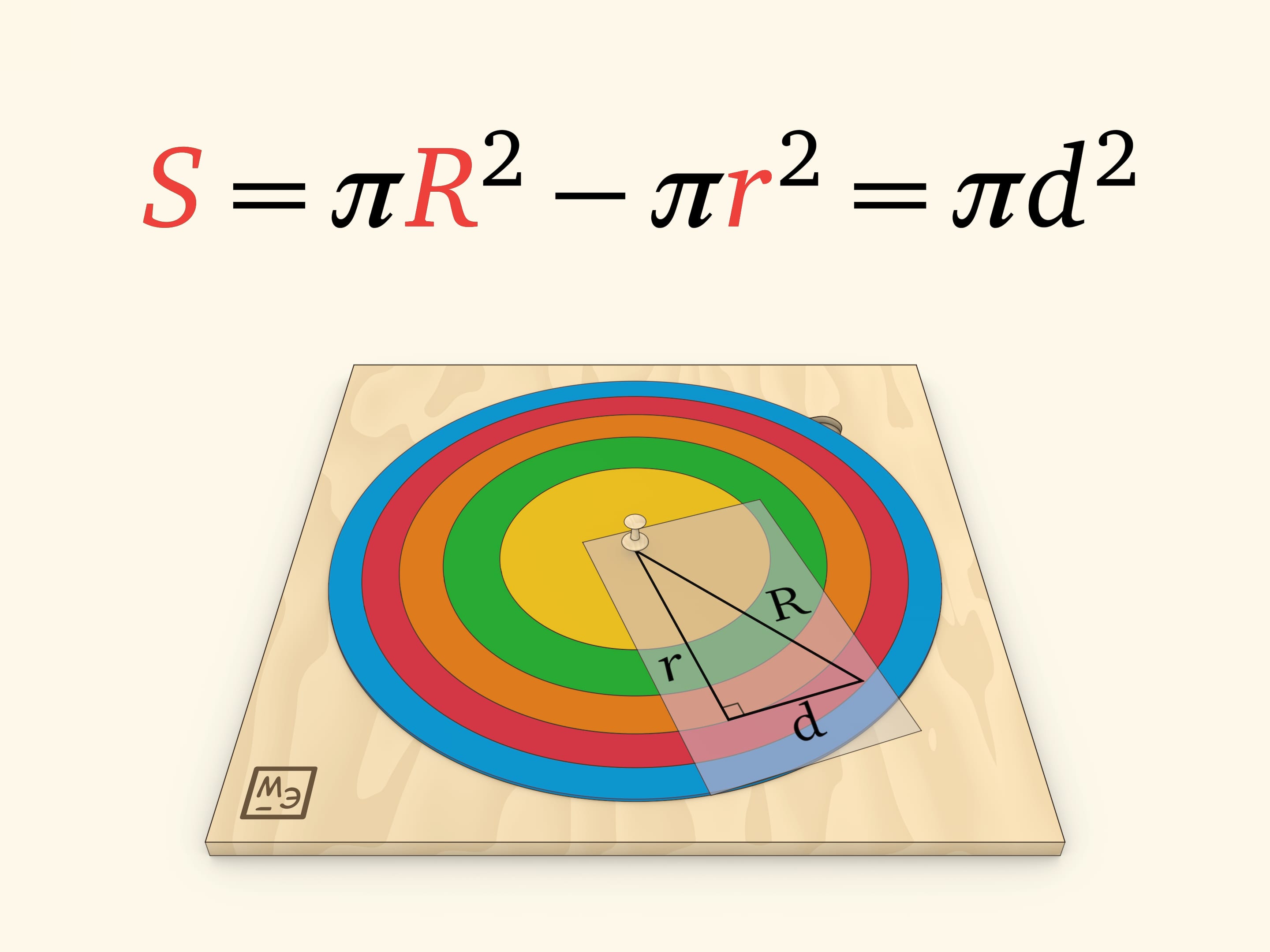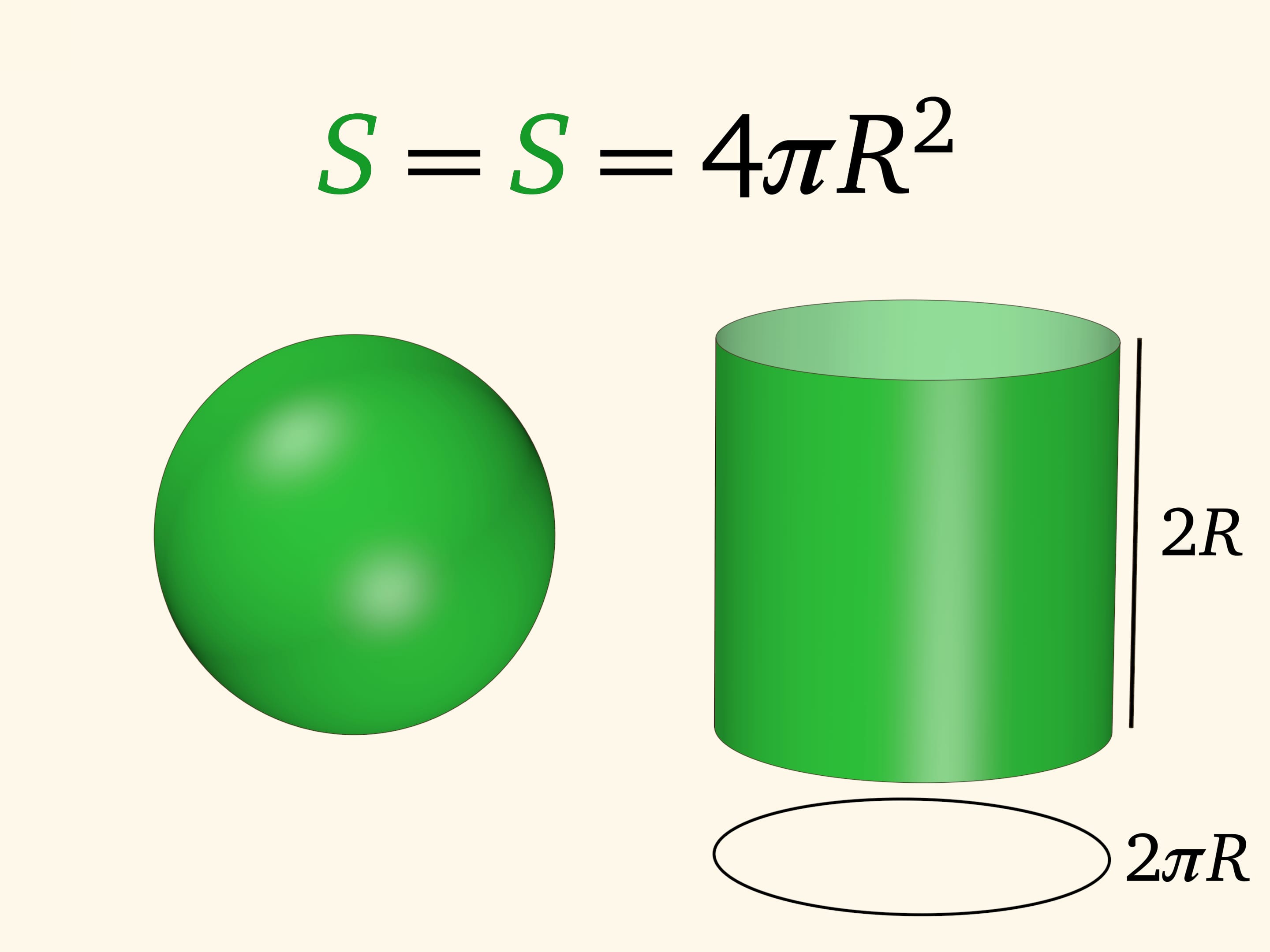Если разрезать мякоть персика где-то рядом с концом косточки, а затем около экватора, — в каком месте площадь мякоти будет больше? «Теорема о косточке» утверждает, что площадь среза будет одинакова: она не зависит от уровня среза!
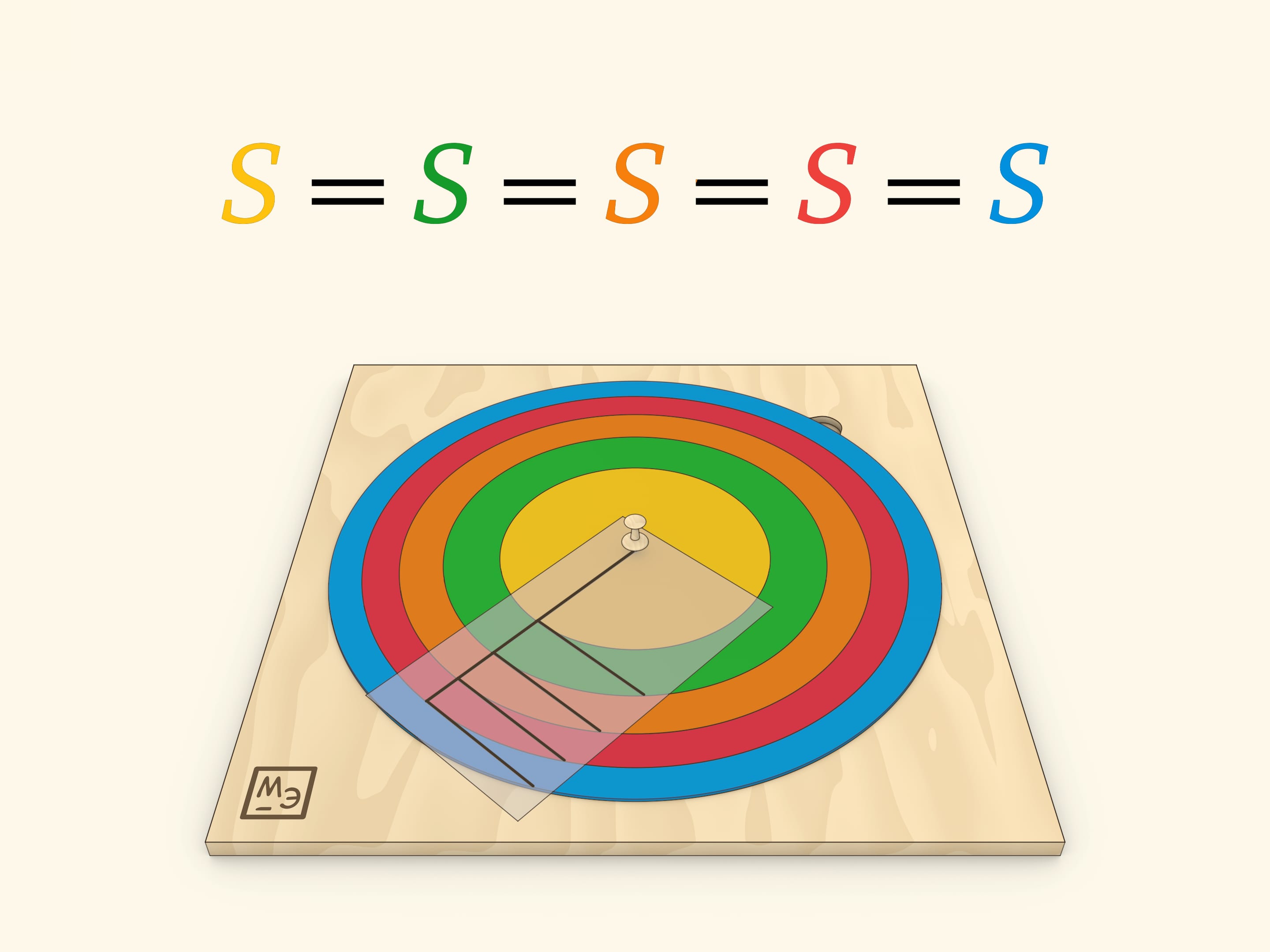
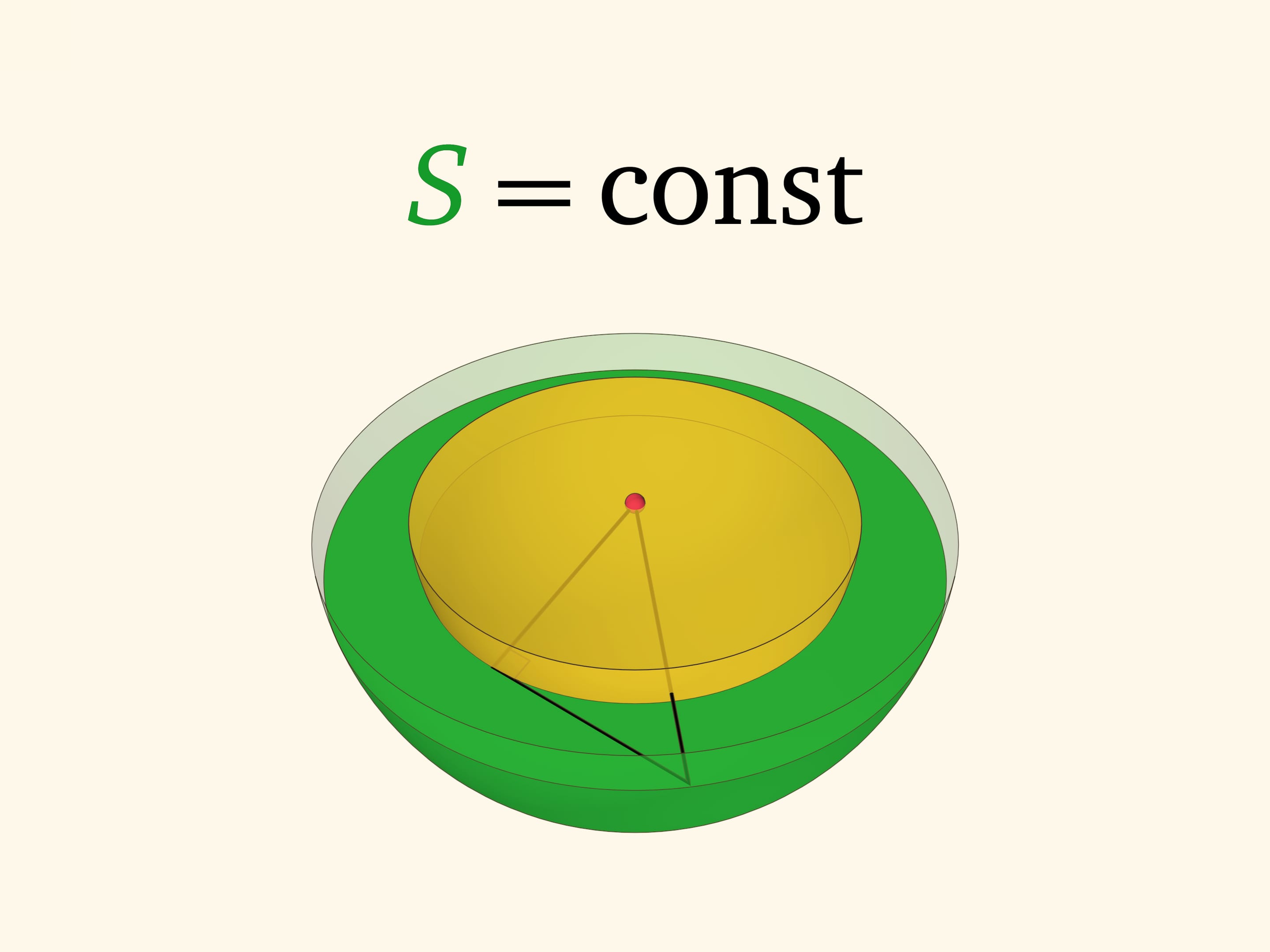
Модель круга, разделённого на кольца равной площади, можно встретить в различных музеях математики. Первое очевидное наблюдение: чем кольцо дальше от центра, тем оно у́же. А дополняет модель «прозрачка» с отмеченными касательными, идущими внутри каждого кольца. Второе, уже не столь очевидное наблюдение: длины отмеченных отрезков равны.
Удивительный факт: площадь кольца определяется только длиной этого касательного отрезка, заметающего кольцо. Убедиться в этом можно, воспользовавшись теоремой Пифагора.
Сформулированное утверждение о площади кольца представляет собой простейший случай «велосипедной теоремы Мамикона»: если велосипед с рамой длины $d$ проехал так, что следы и от переднего, и от заднего колеса образуют замкнутые кривые, то заключённая между ними площадь не зависит от того, что это за кривые, и всегда равна $\pi d^2$. (Считается, что заднее колесо не проскальзывает и поэтому рама во всех точках является касательной к следу заднего колеса.) В нашем случае рама велосипеда — рассмотренный отрезок касательной, траектория заднего колеса — меньшая окружность кольца, а переднего — большая окружность кольца; площадь кольца определяется только длиной $d$.
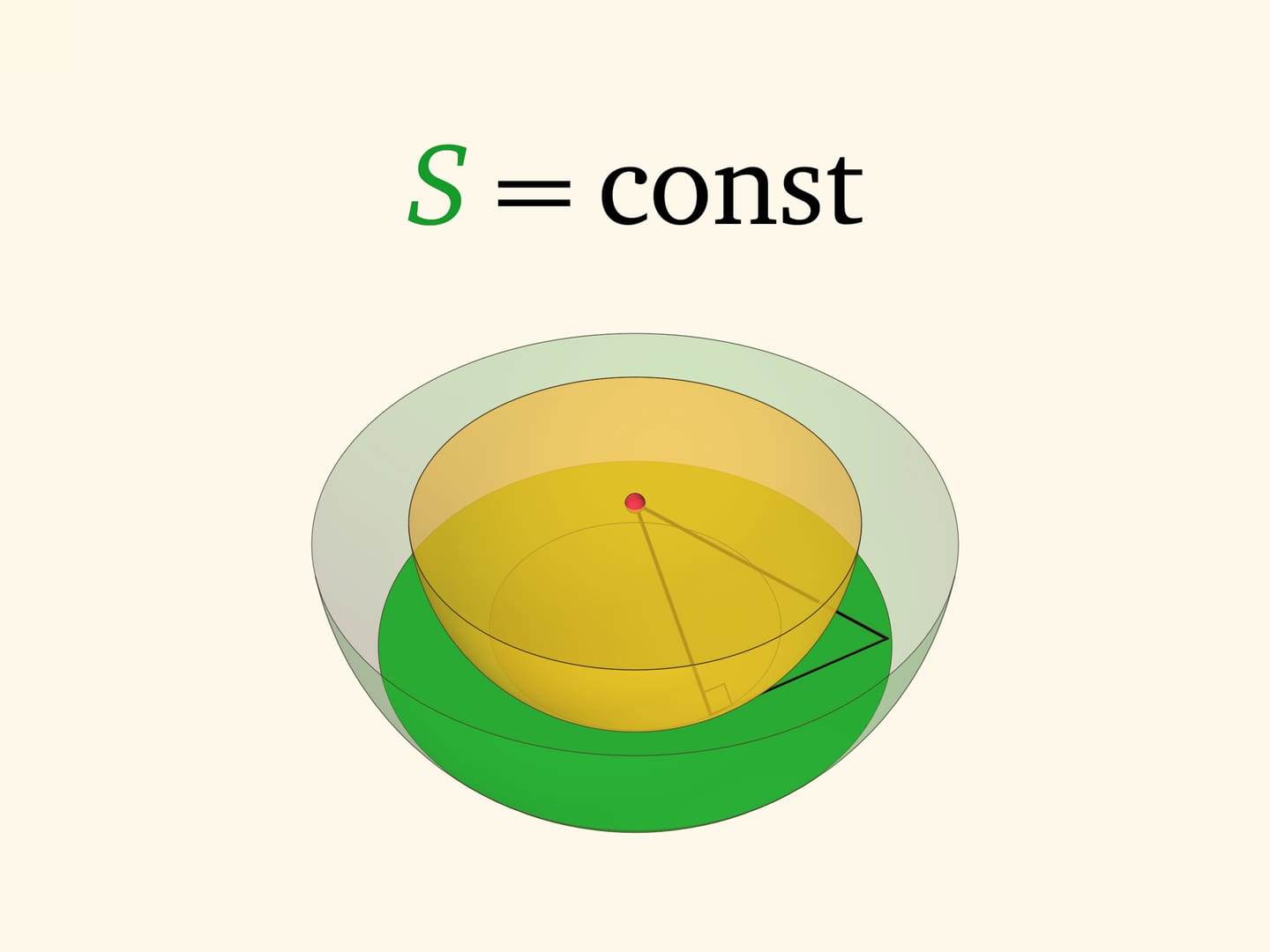
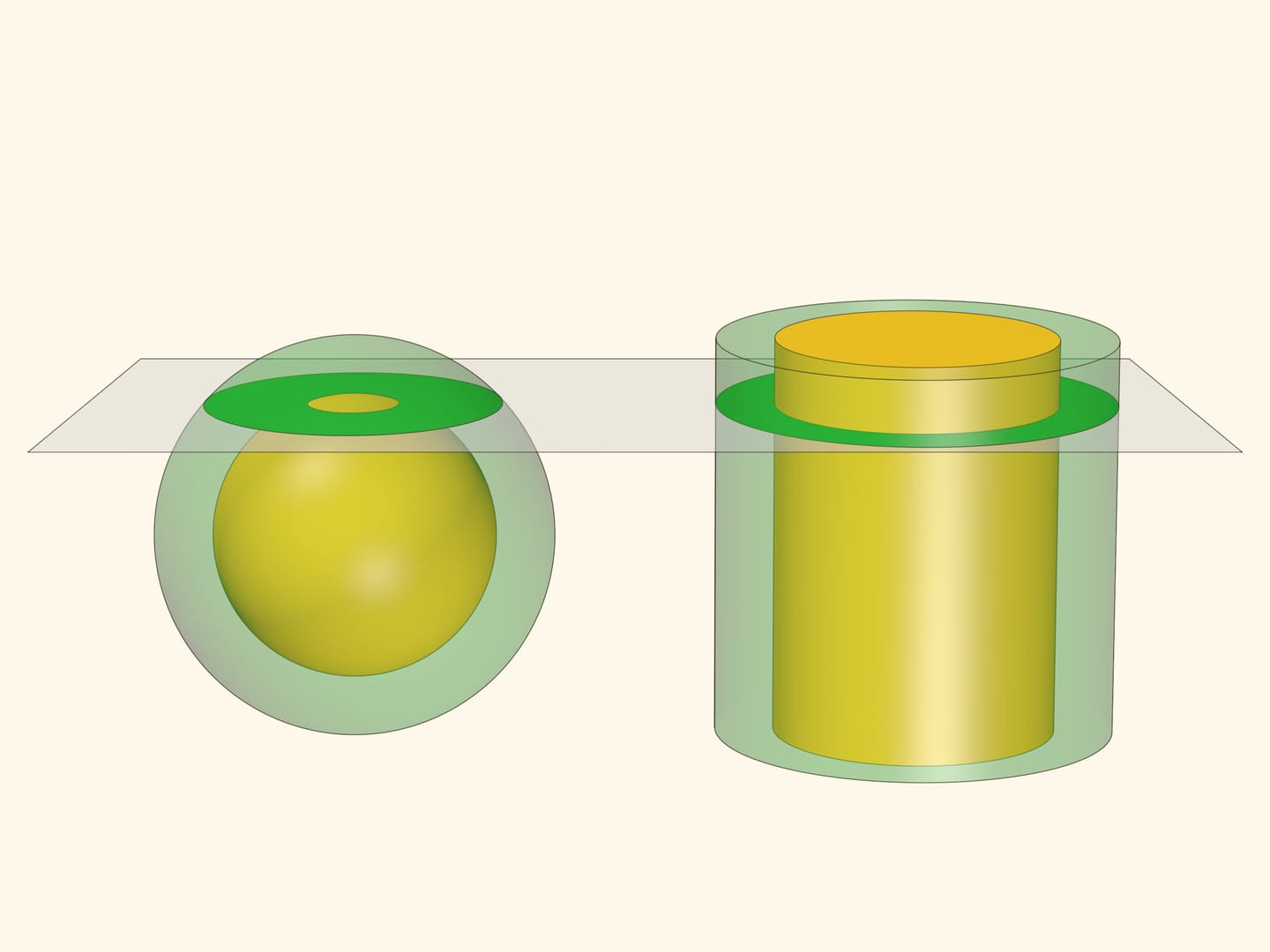
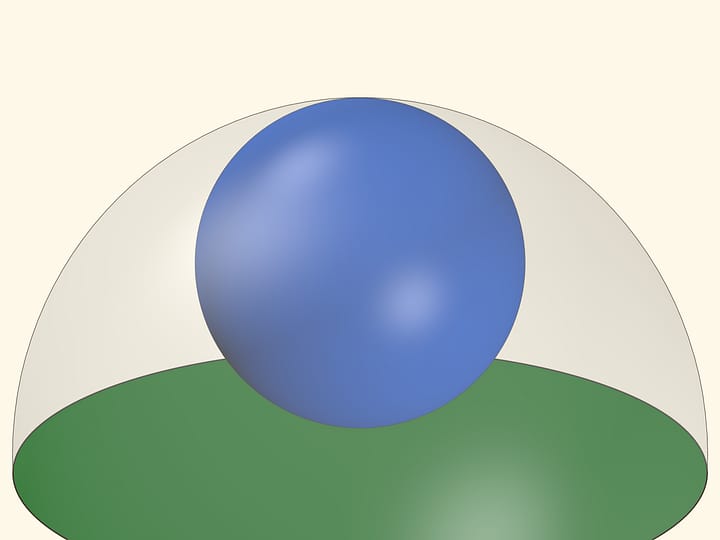
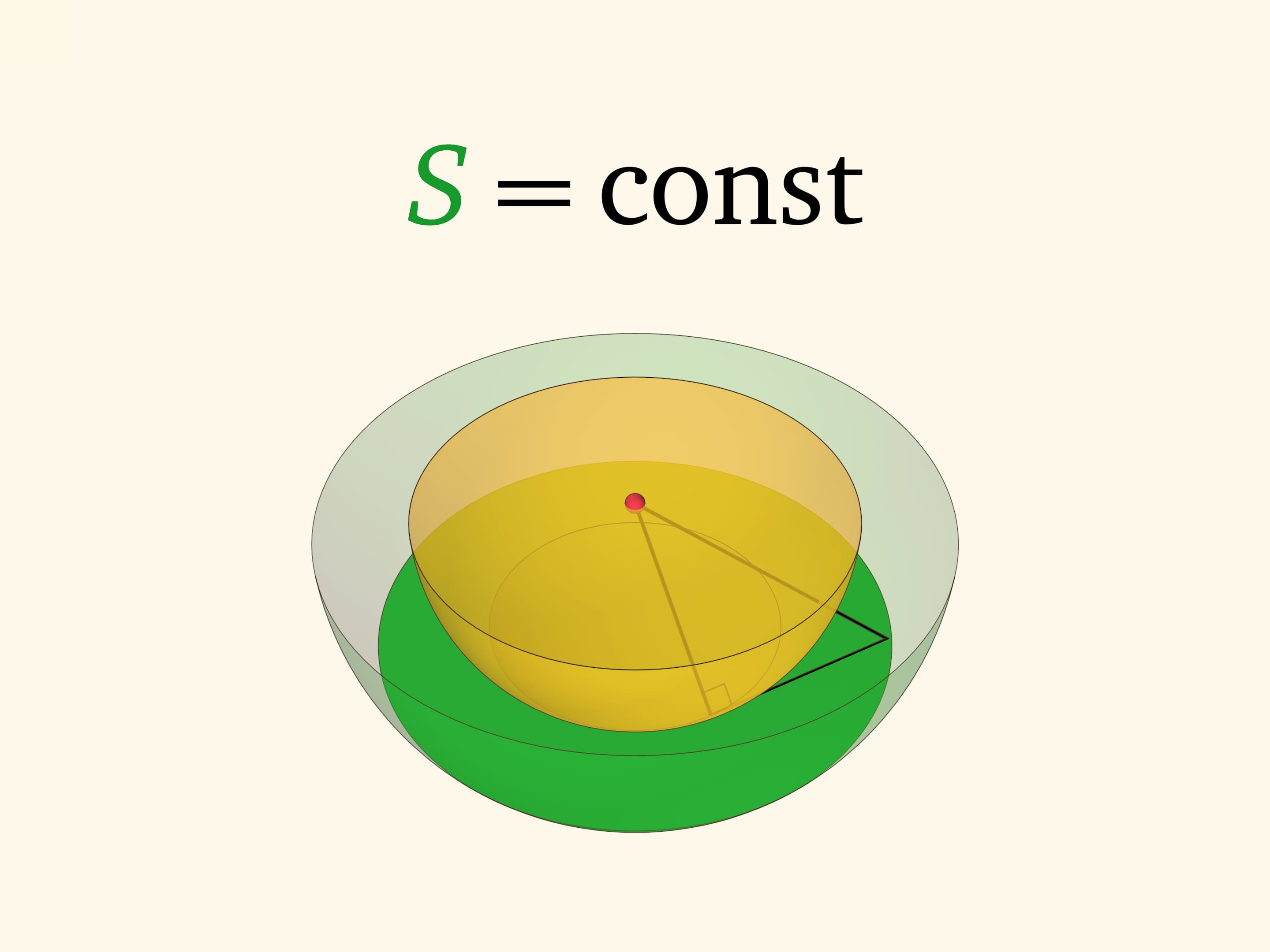
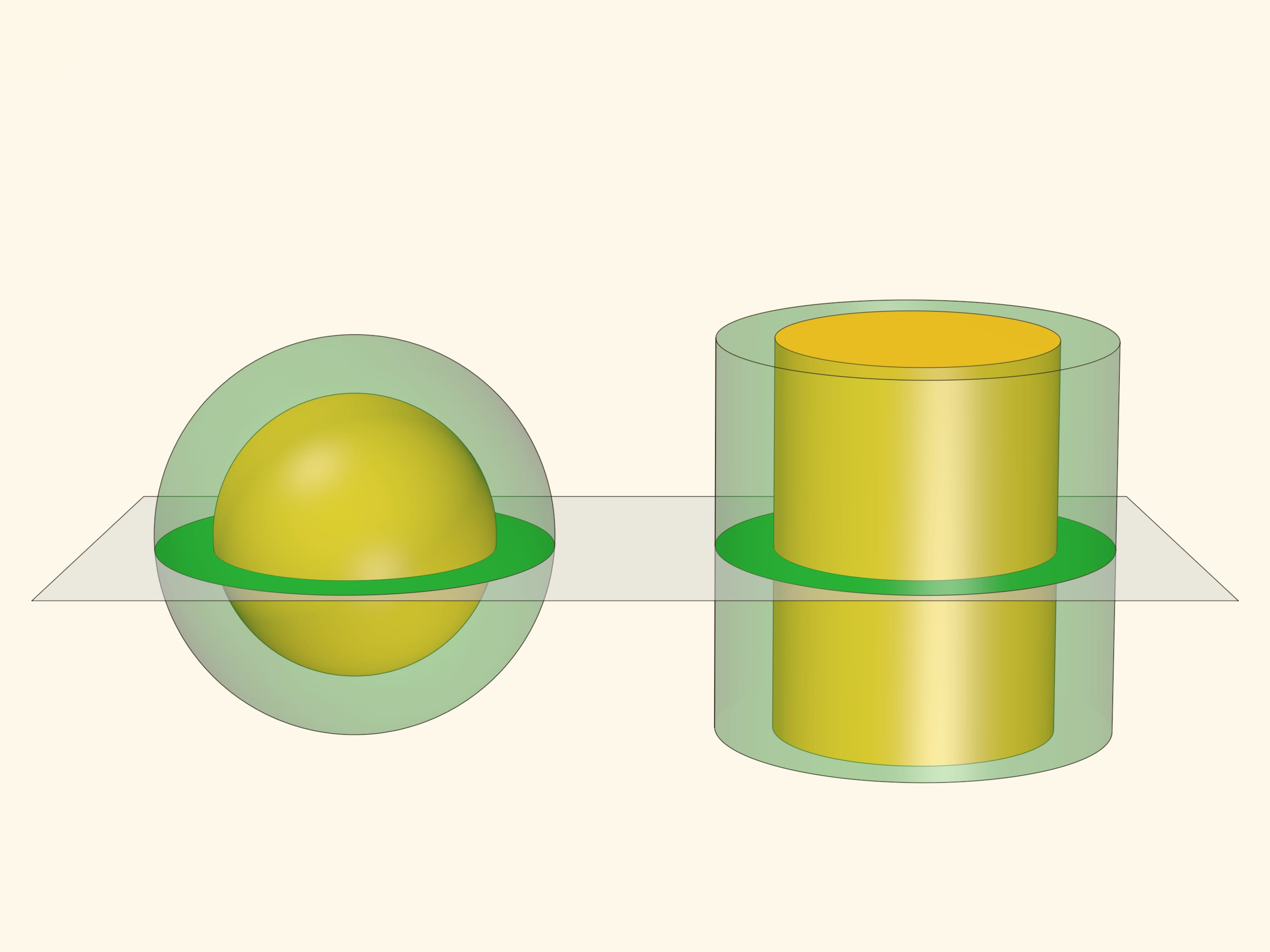
Зависимость площади кольца только от длины касательной имеет интересное следствие в трёхмерном пространстве. Представим, что на центральном круге рассмотренной модели и следующем кольце построены концентрические сферы (полусферы). Внутренняя сфера — математический образ косточки, внешняя — поверхности персика. Площадь «мякоти» на срезе — площадь кольца между сферами при сечении плоскостью, захватывающем внутреннюю сферу.
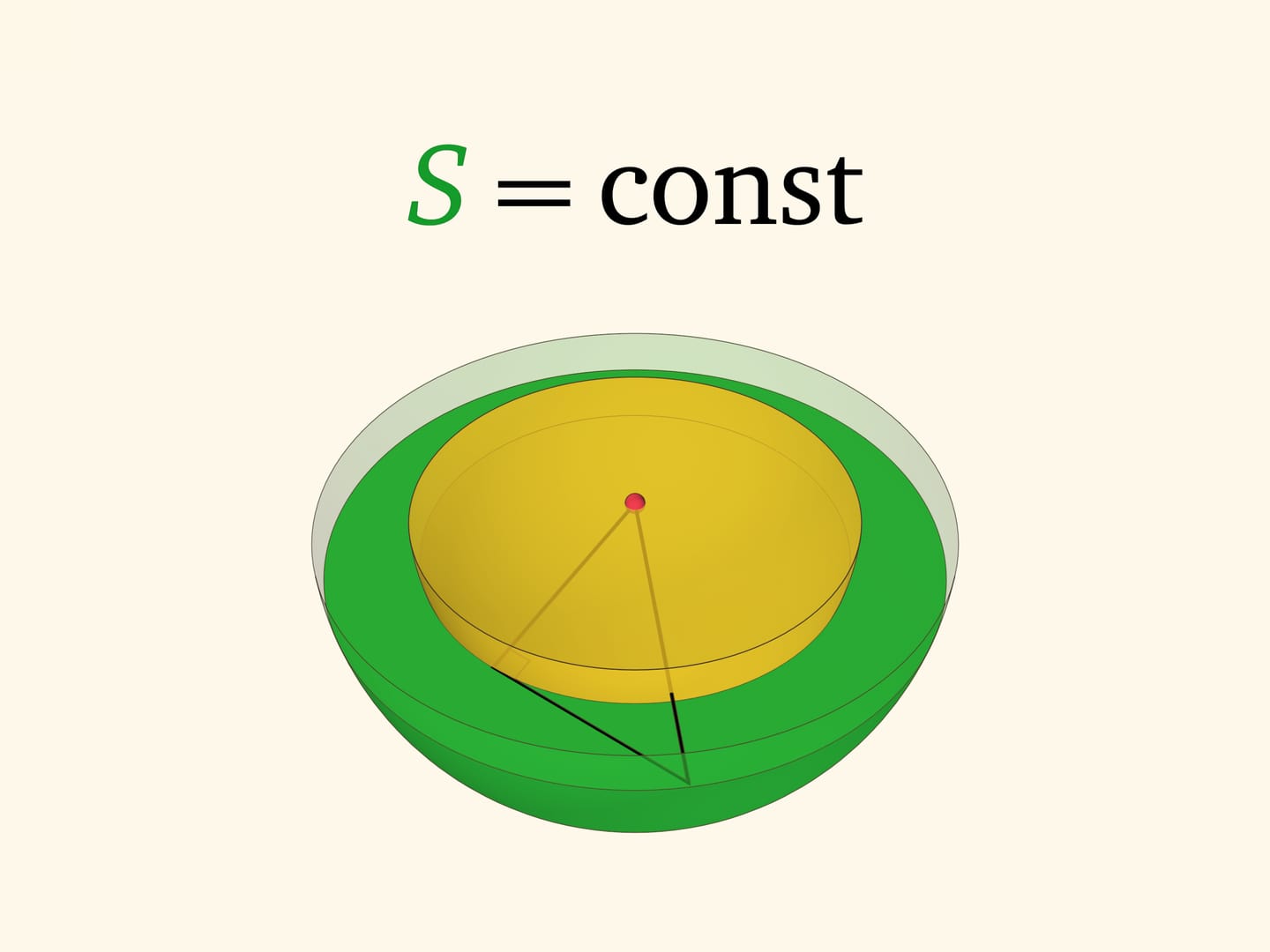
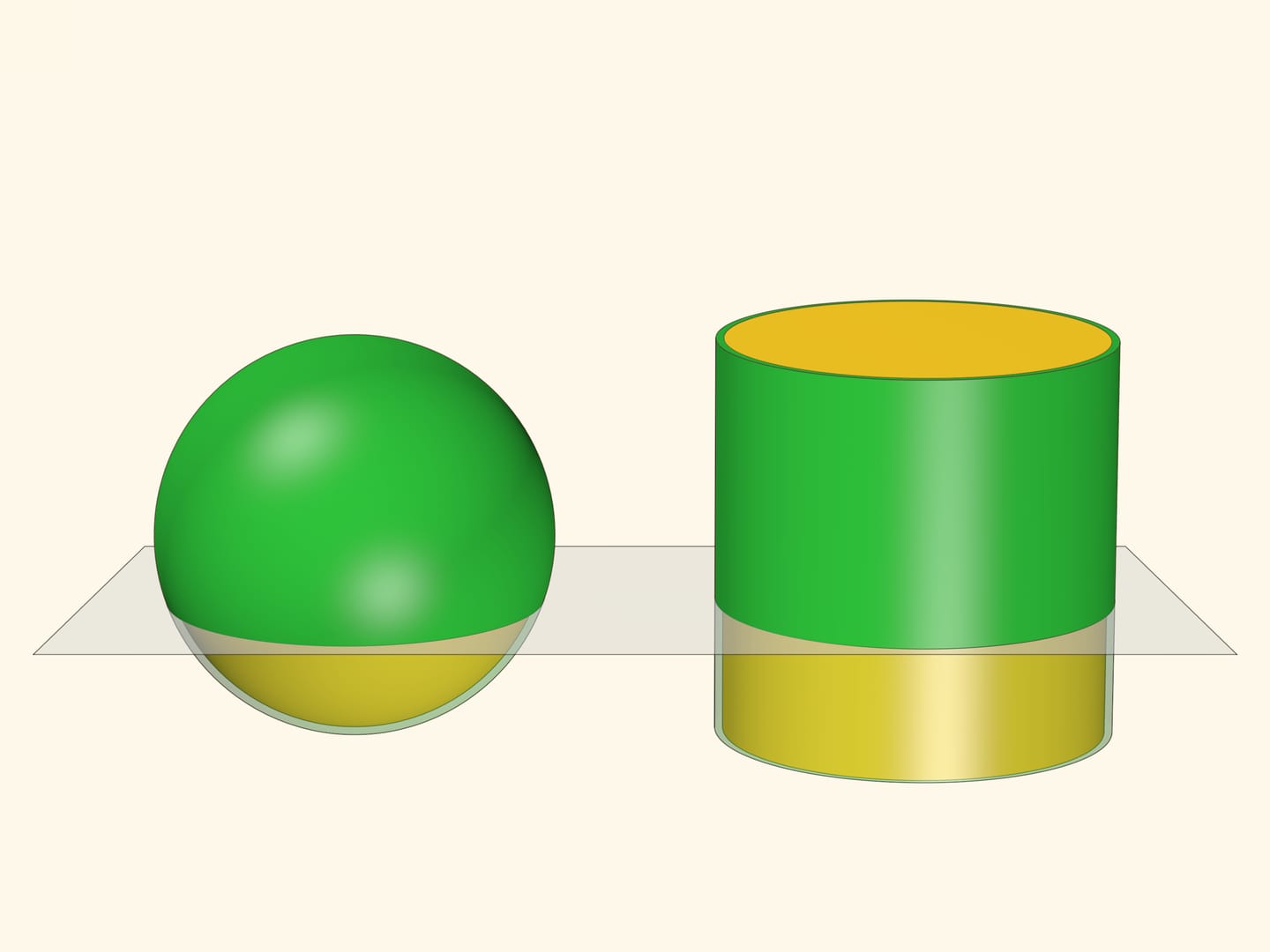
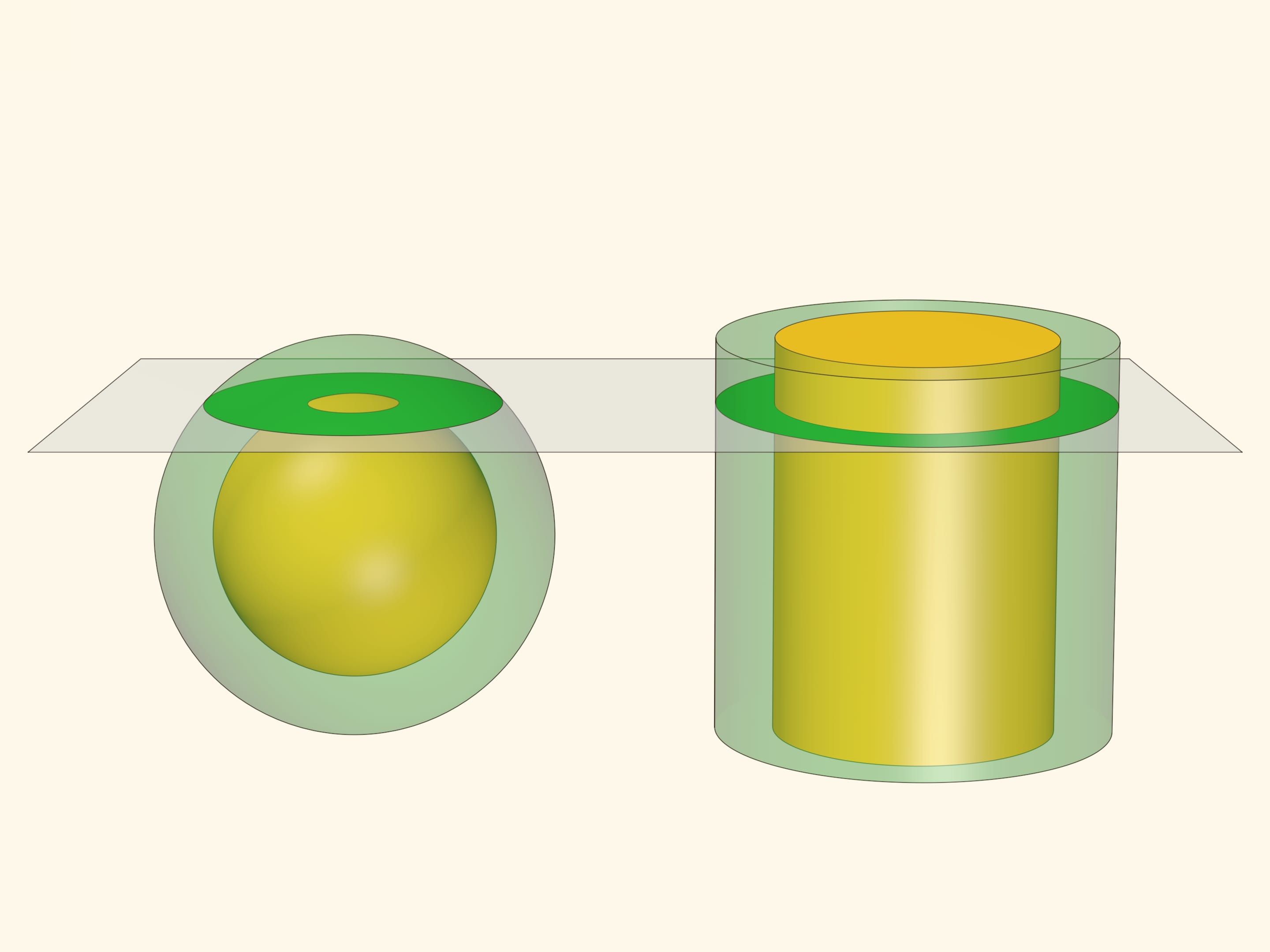
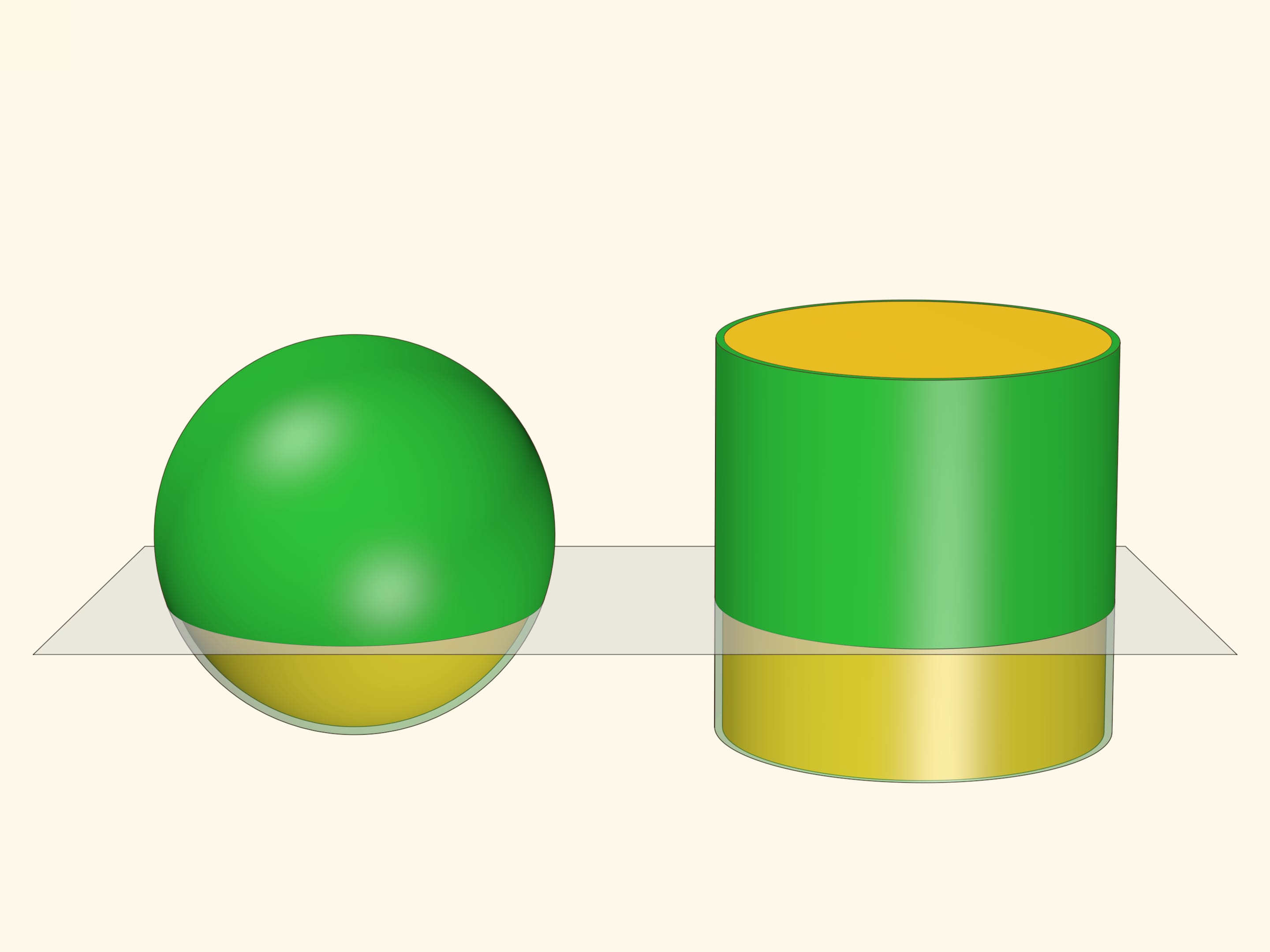
Проследим, как площадь кольца зависит от уровня секущей плоскости. Для этого рассмотрим прямоугольный треугольник с вершиной в центре сфер и одним катетом, лежащим в кольце и касательным к внутренней сфере. Площадь кольца, как мы уже знаем, определяется только длиной этого катета — того самого отрезка $d$ из плоского случая, «дощечки». Две другие стороны прямоугольного треугольника постоянны — равны радиусам сфер. А значит, длина рассматриваемого катета не зависит от уровня сечения. Площади всех колец одинаковы и не зависят от уровня плоскости: площадь «узкого» кольца у экватора и площадь «широкого» кольца, лишь немного захватывающего косточку, — равны!
Сформулированная «теорема о косточке» позволяет посчитать площадь сферы. Для этого вместе с двумя концентрическими сферами рассмотрим два «концентрических» цилиндра с радиусами, равными радиусам сфер, и высотой, равной диаметру внешней сферы. В сечении, перпендикулярном оси цилиндров, площадь кольца между сферами равна площади кольца между цилиндрами и эти площади остаются постоянными вне зависимости от уровня плоскости.
При приближении радиуса внутренних фигур к внешним объём «мякоти» становится всё меньше. В какой-то момент этот объём можно представлять себе как объём краски, наносимой на поверхность. Как говорят, «в пределе» этот объём перейдёт в площадь рассматриваемых тел. И значит, площадь сферы равна площади цилиндра того же радиуса и высоты. Но площадь цилиндра — поверхности, разворачиваемой на плоскость, — подсчитывается легко: произведение длины окружности в основании на длину высоты. Значит, площадь сферы радиуса $R$ равна $4\pi R^2$.
Литература
Мерзон Г. Пифагор на велосипеде // Журнал «Квантик». — 2019. — № 8. — Стр. 16—17.
Акопян А. Апельсины, канализационные люки и разрезание длинного прямоугольника // Журнал «Квант». — 2021. — № 9. — Стр. 40—43.
Apostol Tom M., Mnatsakanian Mamikon A. New Horizons in Geometry. — Mathematical Association of America, 2013. — ISBN 9781614442103.
Площадь на сфере: сферы, шапочки, кольца // Математические этюды.