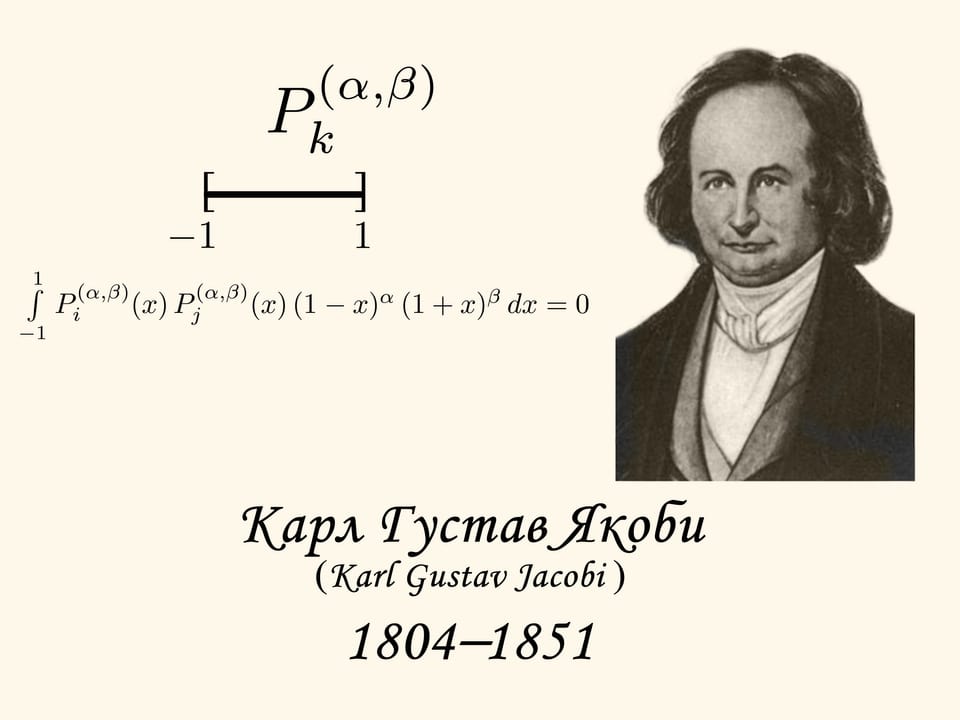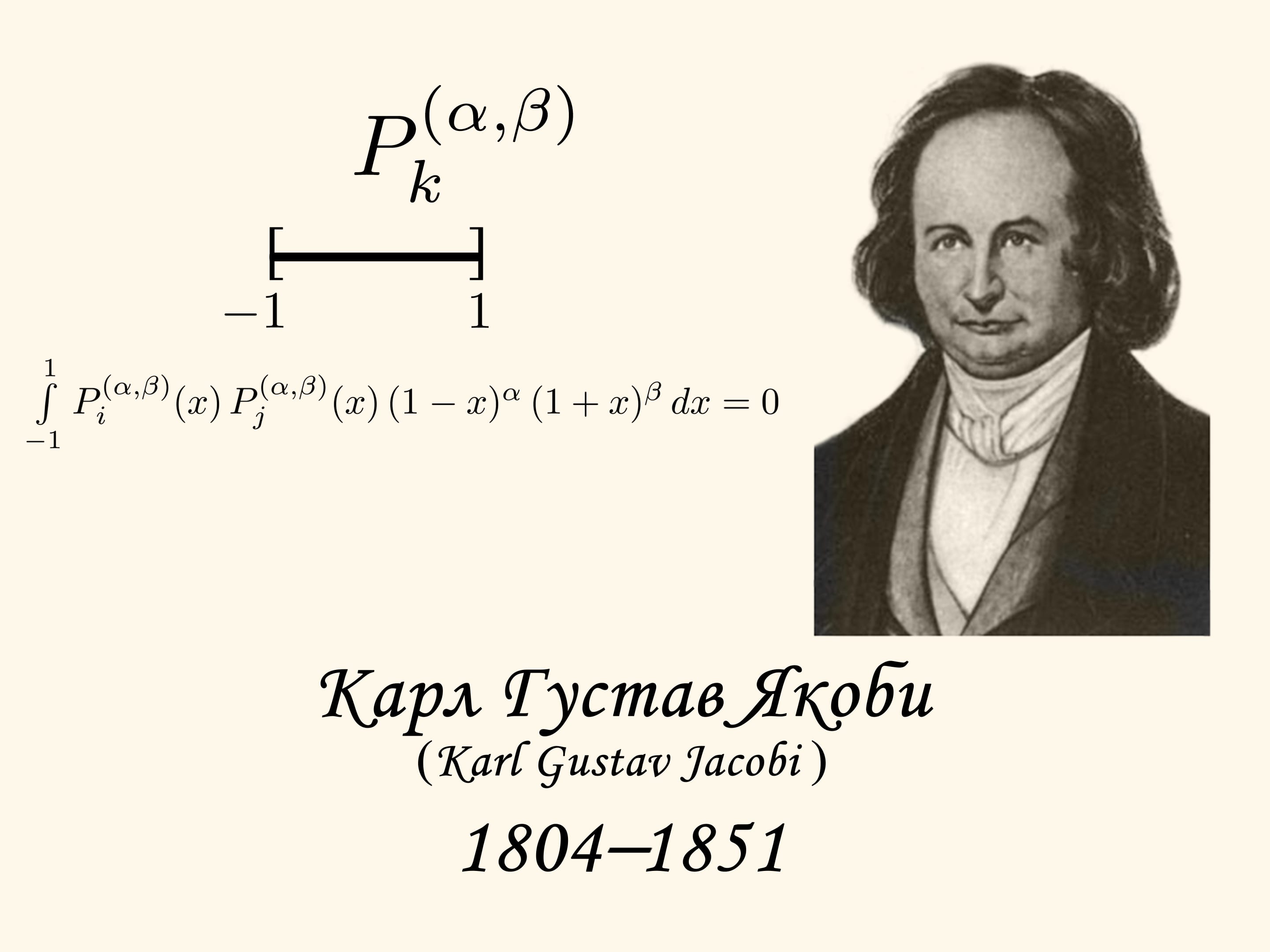Хорошая конструкция ⁠

Карл Густав Якоби жил в пер­вой поло­вине XIX века. Для своих есте­ствен­но­на­уч­ных иссле­до­ва­ний он раз­ра­бо­тал систему ортого­наль­ных много­чле­нов, кото­рые потом полу­чили его имя. При задан­ных зна­че­ниях парамет­ров $\alpha$ и $\beta$ (больших чем $-1$) много­член Якоби $P_{k}^{(\alpha, \beta)}$ явля­ется много­чле­ном степени $k$ и имеет столько же нулей на отрезке $[-1,1].$

Поня­тие ортого­наль­но­сти, т. е. перпен­ди­ку­ляр­но­сти, пере­ко­че­вало из геомет­рии и в другие обла­сти матема­тики. Если два век­тора перпен­ди­ку­лярны, то их ска­ляр­ное про­из­ве­де­ние равно нулю. По ана­логии, два много­члена назы­ваются ортого­наль­ными, если их ска­ляр­ное про­из­ве­де­ние равно нулю. Только в нашем слу­чае под ска­ляр­ным про­из­ве­де­нием понима­ется интеграл по отрезку $[-1,1]$ от про­из­ве­де­ния рас­смат­ри­ва­емых много­чле­нов, умножен­ного на спе­ци­аль­ную функцию, назы­ва­емую весом.

Системы ортого­наль­ных много­чле­нов играют большую роль в самой матема­тике и в при­клад­ных вопро­сах. Воз­ни­кающие в процессе иссле­до­ва­ния функции, свойства кото­рых необ­хо­димо изу­чить, можно с той или иной степе­нью точ­но­сти при­бли­зить линей­ной ком­би­нацией рас­смат­ри­ва­емых ортого­наль­ных много­чле­нов. Далее можно изу­чать уже пове­де­ние не самой функции, а при­ближающей кон­струкции, что зача­стую суще­ственно проще и удоб­нее.

Изу­че­ние ортого­наль­ных много­чле­нов и их свойств — это большой и инте­рес­ный раз­дел матема­тики, имеющий и важ­ное при­клад­ное зна­че­ние.

Как это зача­стую бывает в науке, некогда выдуман­ная хорошая кон­струкция нахо­дит инте­рес­ные при­ме­не­ния в раз­лич­ных вопро­сах. Так и много­члены Якоби, а точ­нее, их нули, ока­за­лись реше­нием важ­ной задачи, воз­никшей суще­ственно позд­нее, нежели были вве­дены сами рас­смат­ри­ва­емые много­члены.

Пусть на кон­цах отрезка $[-1,1]$ закреп­лены положи­тель­ные заряды вели­чины $q$ и $p.$ Внутри отрезка слу­чай­ным обра­зом поме­стили $k$ еди­нич­ных заря­дов, кото­рые могут сво­бодно перемещаться по нему, но поки­дать отре­зок им запрещено. Так как заряды оди­на­ко­вого знака, то они ста­раются раз­бежаться как можно дальше друг от друга. Как рас­по­ложатся заряды, пыта­ясь мини­ми­зи­ро­вать потенци­аль­ную энергию системы? В нахож­де­нии оптималь­ного рас­по­ложе­ния, когда силы, действующие на каж­дый заряд справа и слева, равны, и состоит задача.

Для зна­ком­ства с зада­чей рас­смот­рим част­ные слу­чаи.

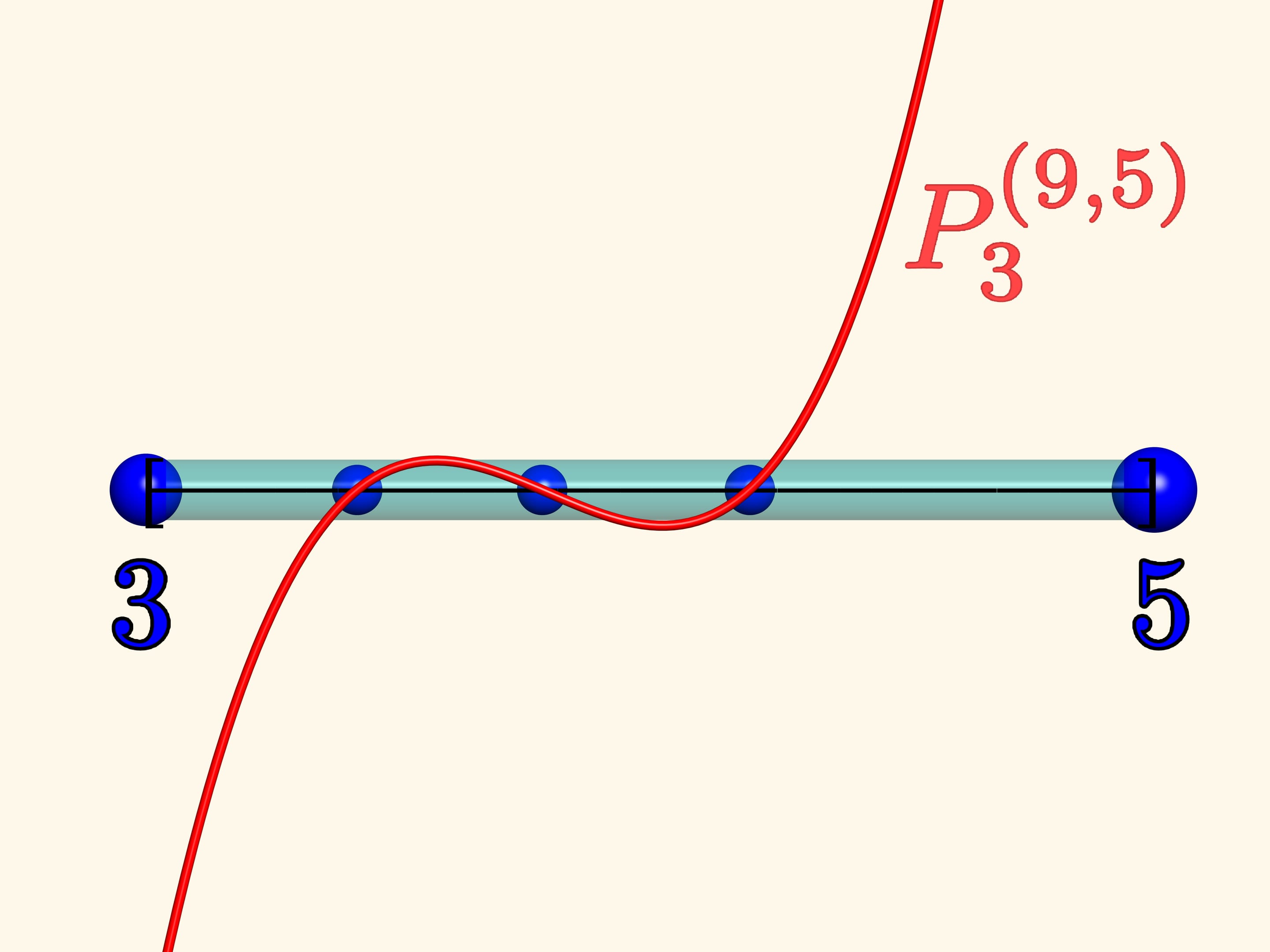
Пусть на левом конце отрезка закреп­лен заряд, рав­ный $3$, а на пра­вом — рав­ный $5.$ Поста­вим в про­из­воль­ные точки три еди­нич­ных заряда, имеющих возмож­ность сво­бодно перемещаться по отрезку, и посмот­рим на пове­де­ние системы. Когда движе­ние оста­но­вится, нари­суем на том же отрезке график много­члена Якоби $P_{3}^{(9, 5)}.$ Ока­зы­ва­ется, что заряды оста­но­ви­лись в нулях этого много­члена!

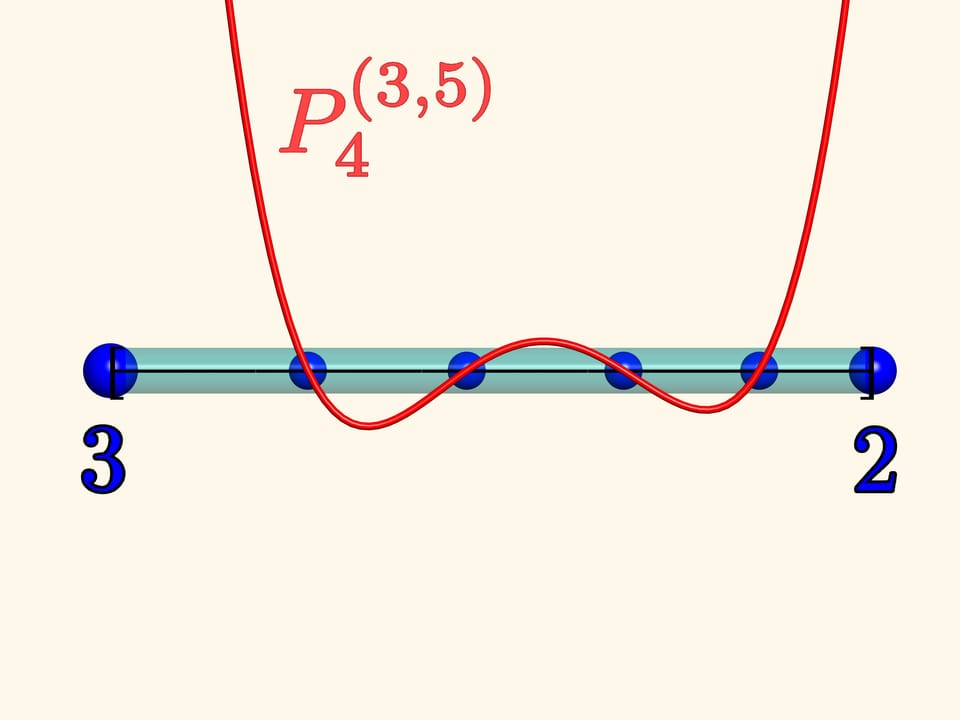
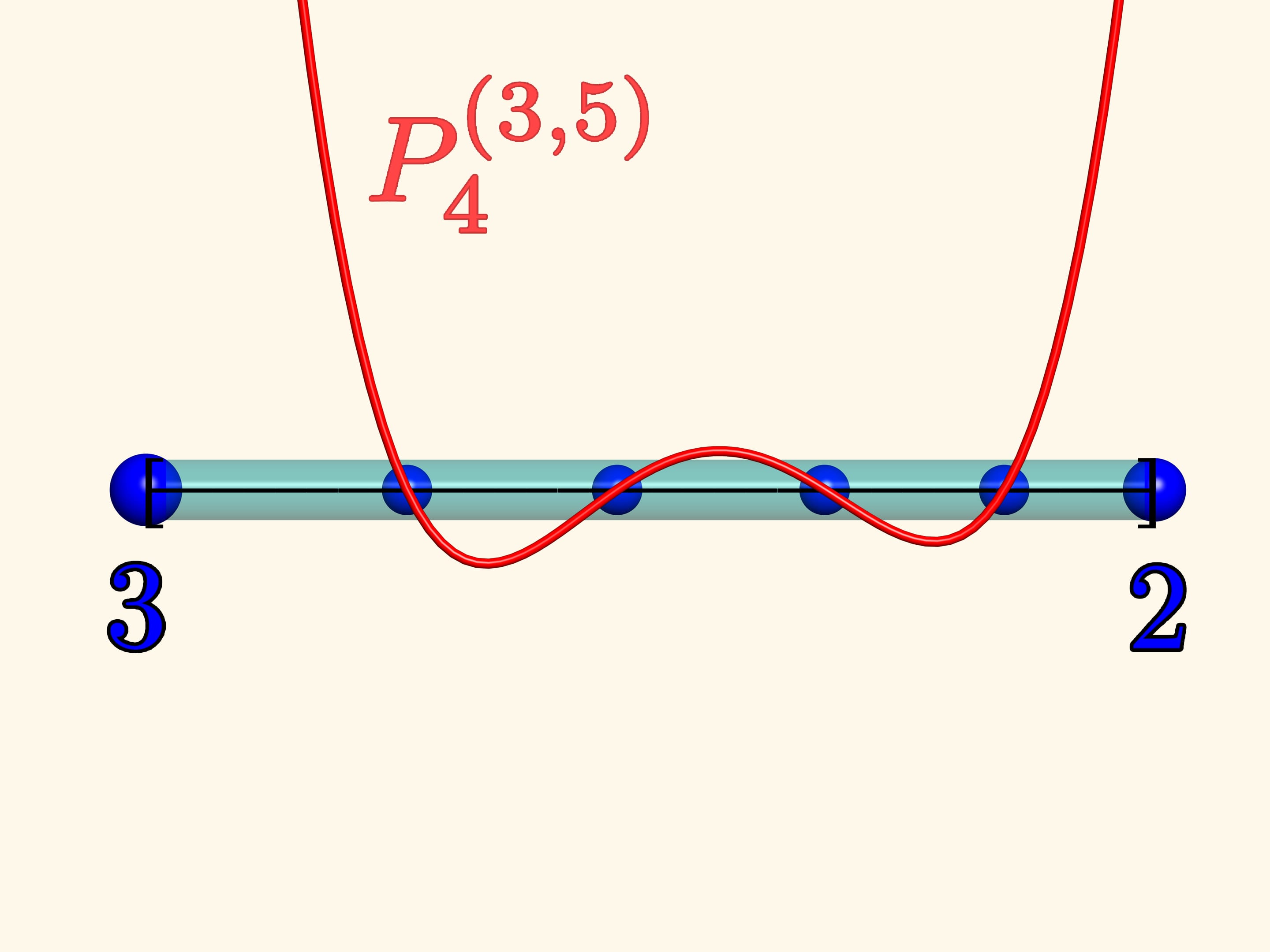
Давайте проэкс­пе­ремен­ти­руем ещё раз. Зафик­си­руем на левом конце заряд, рав­ный $3$, а на пра­вом — рав­ный $2.$ Поме­стим внутри отрезка четыре еди­нич­ных заряда и пона­блю­даем за системой. Когда заряды пере­ста­нут двигаться, они окажутся в нулях много­члена Якоби $P_{4}^{(3, 5)}.$

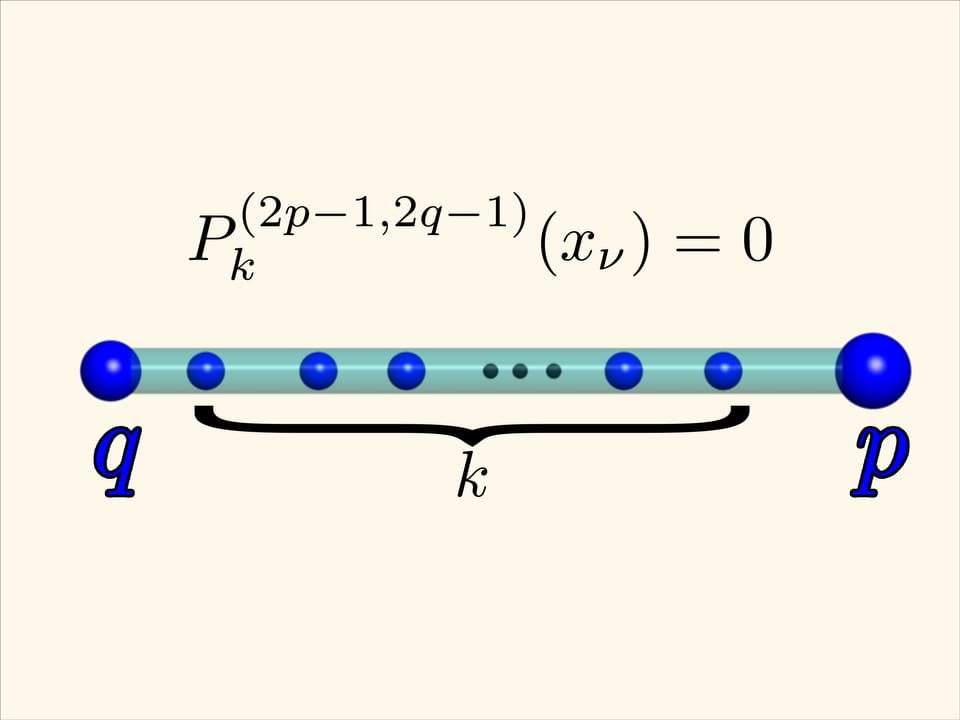
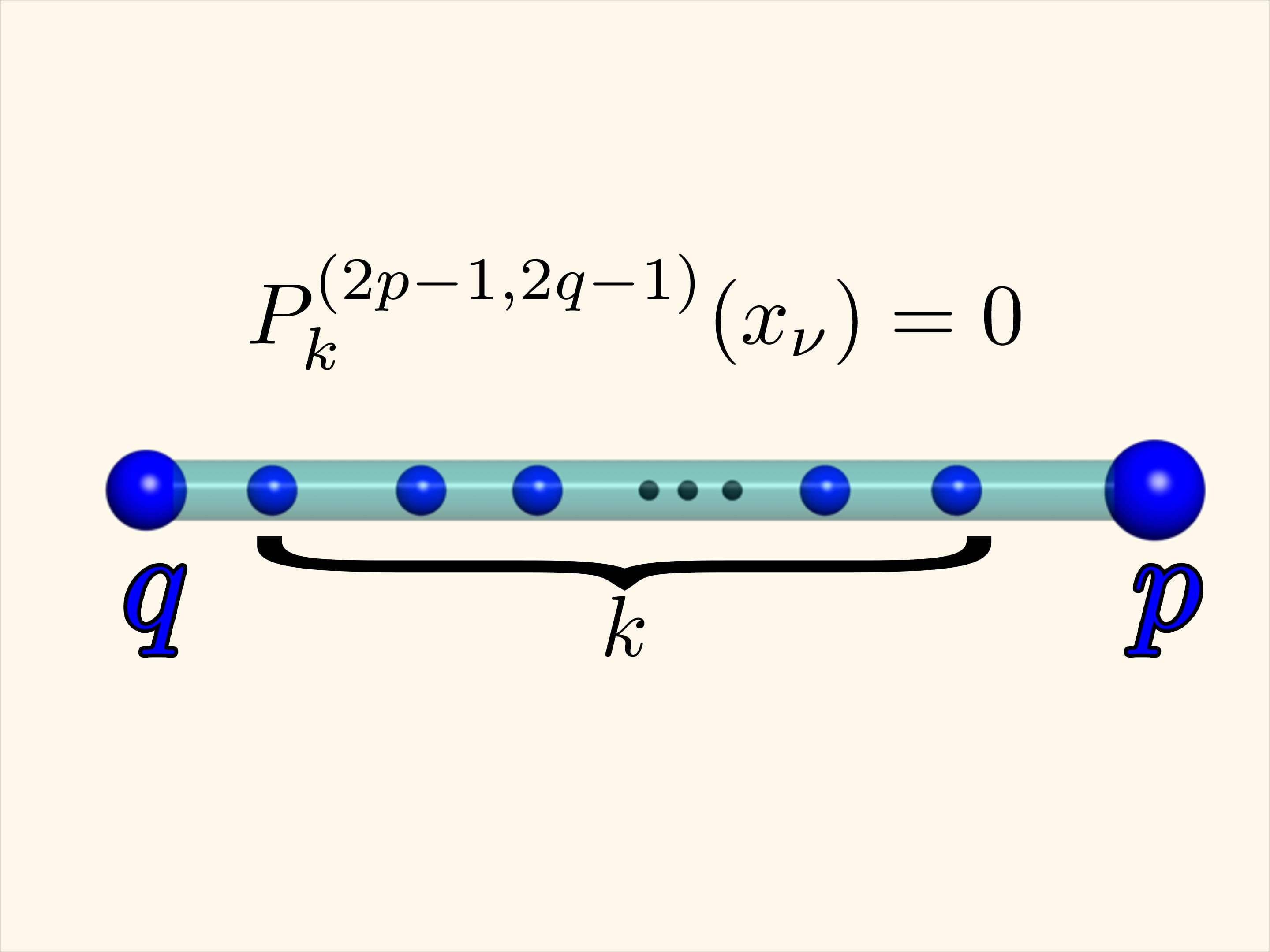
В общем слу­чае наблю­да­емая зави­симость тоже верна. Если на левом конце отрезка $[-1,1]$ нахо­дится заряд, рав­ный $q$, а на пра­вом — рав­ный $p$, между ними нахо­дятся $k$ еди­нич­ных заря­дов, то минимум потенци­аль­ной энергии такой системы будет достигаться, если «внут­рен­ние» заряды будут рас­по­ложены в нулях много­члена Якоби $P_{k}^{(2p-1, 2q-1)}.$

Вот так некогда при­думан­ная система ортого­наль­ных много­чле­нов Якоби воз­никла при реше­нии задачи из совершенно дру­гой есте­ственно-науч­ной обла­сти. А также про­яв­ляет свои свойства и во многих других зада­чах, как и любая «хорошая кон­струкция».